Class 12th

The area of the region, enclosed by the circle x² + y² = 2, which is not common to the region bounded by the parabola y² = x and the straight line y = x, is:

0 Follower 6 Views

Contributor-Level 10

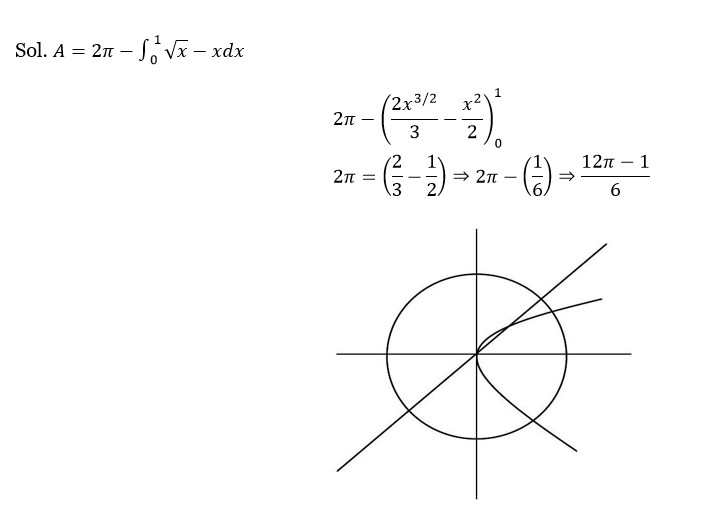
Area A = 2π - ∫? ¹ (√x - x) dx is incorrect. The area is likely between two curves.
The calculation shown is:
A = 2π - [2/3 x^ (3/2) - x²/2] from 0 to 1.
A = 2π - (2/3 - 1/2) = 2π - (4/6 - 3/6) = 2π - 1/6 = (12π - 1)/6.

0 0

New answer posted

4 months ago

If y = y(x) is the solution of the differential equation, e?(dy/dx – 1) = e? such that y(0) = 0, then y(1) is equal to:

0 Follower 11 Views

Contributor-Level 10

0 0

New answer posted

4 months ago

If for a > 0, the feet of perpendiculars from the points A(a, -2a, 3) and B(0, 4, 5) on the plane lx + my + nz = 0 are points C(0, -a, -1) and D respectively, then the length of line segment CD is equal to :

0 Follower 3 Views

Class 12th Differential Equations

Contributor-Level 9

AC is collinear with l, m, n.
(l/a) = (m/-a) = (n/4) = λ.
Again (0, -a, -1) lies on lx + my + nz = 0.
l (0) + m (-a) + n (-1) = 0 ⇒ -am - n = 0
-a (-aλ) - (4λ) = 0 ⇒ a²λ - 4λ = 0 ⇒ a² = 4, a = ±2.
for a > 0, a = 2. Direction ratios of BD are 2, -2, 4.
Equation of BD: x/2 = (y - 4)/-2 = (z - 5)/4 = r.
Any point on it (2r, 4 - 2r, 5 + 4r) lies on plane lx + my + nz = 2x - 2y + 4z = 0.
⇒ 4r - 2 (4 - 2r) + 4 (5 + 4r) = 0 ⇒ 24r + 12 = 0 ⇒ r = -1/2.
∴ D (-1, 5, 3), C (0, -2, -1).
∴ CD = √ (0 - (-1)² + (-2 - 5)² + (-1 - 3)²) = √ (1 + 49 + 16) = √66

0 0

New answer posted

4 months ago

Let xᵏ + yᵏ = aᵏ, (a, k > 0) and dy/dx + (y/x)¹/³ = 0, then k is:

0 Follower 4 Views

Contributor-Level 10

Given kx^ (k-1) + k * y^ (k-1) * dy/dx = 0.
dy/dx = - (kx^ (k-1) / (ky^ (k-1) = - (x/y)^ (k-1).
The provided solution has dy/dx + (x/y)^ (k-1) = 0.
It seems to relate to k-1 = -1/3, which implies k = 1 - 1/3 = 2/3.

0 0

New answer posted

4 months ago

Let α be a root of the equation x² + x + 1 = 0 and the matrix A = (1/√3) [, [1, α, α²], [1, α², α⁴]], then the matrix A³¹ is equal to:

0 Follower 5 Views

Contributor-Level 10

A = 1/3 [ 1; 1 ω ω² 1 ω² ω ]
A² = A * A = 1/9 [ . ]
(The calculation in the image shows A² is the identity matrix, let's verify)
A² leads to I (Identity matrix).
So A² = I.
A³ = A² * A = I * A = A.
A? = (A²)² = I² = I.
A³? = (A²)¹? = I¹? = I.

0 0

New answer posted

4 months ago

If y = y(x) is the solution of the differential equation, dy/dx + 2ytanx = sinx, y(π/3) = 0, then the maximum value of the function y(x) over R is equal to :

0 Follower 4 Views

Contributor-Level 9

dy/dx + 2y tan (x) = sin (x)
I.F. = e^ (∫2tan (x)dx) = e^ (2ln (sec (x) = sec² (x)
Solution is y sec² (x) = ∫sin (x)sec² (x)dx = ∫sec (x)tan (x)dx
⇒ y sec² (x) = sec (x) + c
y (π/3) = 0 ⇒ 0 * sec² (π/3) = sec (π/3) + c ⇒ 0 = 2 + c ⇒ c = -2.
∴ y = (sec (x) - 2) / sec² (x)
Now let g (t) = (t - 2)/t² = 1/t - 2/t² for |t| ≥ 1.
g' (t) = -1/t² + 4/t³
g' (t) = 0 ⇒ t = 4.
g' (t) = 2/t³ - 12/t? g' (4) < 0, hence maximum.
∴ g (t)max = g (4) = (4 - 2)/4² = 2/16 = 1/8.

0 0

New answer posted

4 months ago

Let P be a plane passing through the points (2,1,0), (4,1,1) and (5,0,1) and R be any point (2,1,6). Then the image of R in the plane P is:

0 Follower 7 Views

Contributor-Level 10

The equation of the line is (x-2)/1 = (y-1)/1 = (z-6)/-2.
Let this be equal to k. So, a point on the line is (k+2, k+1, -2k+6).
This point lies on the plane x + y - 2z = 3.
(k+2) + (k+1) - 2 (-2k+6) = 3
2k + 3 + 4k - 12 = 3
6k - 9 = 3
6k = 12 ⇒ k = 2.
The point of intersection is (2+2, 2+1, -2 (2)+6) = (4, 3, 2).

0 0

New answer posted

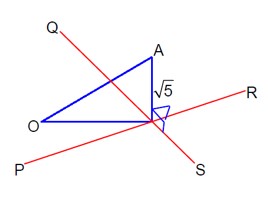
4 months ago

Let the position vectors of two points P and Q be 3i - j + 2k and i + 2j - 4k respectively. Let R and S be two points such that the direction rations of lines PR and QS are (4, -1, 2) and (-2, 1, -2), respectively. Let lines PR and QS intersect at T. If the vector TA is perpendicular to both PR and QS and the length of vector TA is √5 units, then the modulus of a position vector of A is :

0 Follower 4 Views

Contributor-Level 9

PR (line): r = (3i - j + 2k) + λ (4i - j + 2k) - (I)
QS (line): r = (i + 2j - 4k) + μ (-2i + j - 2k) - (II)
If they intersect at T then:
3 + 4λ = 1 - 2μ
-1 - λ = 2 + μ
2 + 2λ = -4 - 2μ
Solving the first two equations gives λ = 2 & μ = -5. These values satisfy the third equation.
∴ T (11, -3, 6)
Also, OT is coplanar with lines PR and QS.
⇒ TA ⊥ OT
|OT| = √166
|TA| = √5
|OA| = √ (|OT|² + |TA|²) = √171

0 0

New answer posted

4 months ago

Class 12th Determinants

If the system of linear equations 2x + 2ay + az = 0, 2x + 3by + bz = 0, 2x + 4cy + cz = 0 where a, b, c ∈ R are non-zero and distinct; has a non-zero solution, then:

0 Follower 2 Views

Contributor-Level 10

0 0

New answer posted

4 months ago

Let the functions f: R → R and g: R → R be defined as :
f(x) = {x+2, x<0; x, x0} and g(x) = {x, x<1; 3x-2, x1}
Then, the number of points in R where (fog)(x) is NOT differentiable is equal to :

0 Follower 4 Views