Class 12th
Get insights from 12k questions on Class 12th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 12th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New question posted
4 months agoNew answer posted
4 months agoContributor-Level 10
We are given bounds for a function f (t) on two intervals and need to find the range of g (3) = ∫? ³ f (t) dt.
We split the integral: g (3) = ∫? ¹ f (t)dt + ∫? ³ f (t)dt.
For the first interval t ∈ [0, 1], we have 1/3 ≤ f (t) ≤ 1. Integrating from 0 to 1 gives:
∫? ¹ (1/3) dt ≤ ∫? ¹ f (t)dt ≤ ∫? ¹ 1 dt ⇒ 1/3 ≤ ∫? ¹ f (t)dt ≤ 1.
For the second interval t ∈ (1, 3], we have 0 ≤ f (t) ≤ 1/2. Integrating from 1 to 3 gives:
∫? ³ 0 dt ≤ ∫? ³ f (t)dt ≤ ∫? ³ (1/2) dt ⇒ 0 ≤ ∫? ³ f (t)dt ≤ (1/2) (3-1) = 1.
Adding the inequalities for the two parts of the integral:
1/3 + 0 ≤ g (3) ≤ 1
New answer posted
4 months agoContributor-Level 9
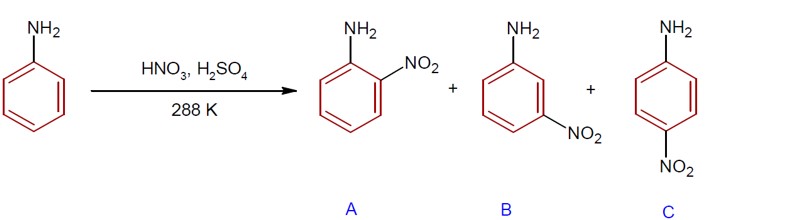
During nitration of aniline, meta- nitroaniline is also formed as product due to formation of –NH? group. The percentage of p, m and o product is 51%, 47% and 2% respectively
New answer posted
4 months agoContributor-Level 10
For a system of linear homogeneous equations to have a non-trivial solution, the determinant of the coefficient matrix must be zero.
Δ = | 4 λ 2 |
| 2 -1 | = 0
| μ 2 3 |
To simplify, perform the row operation R? → R? - 2R? :
Δ = | 0 λ+2 0 |
| 2 -1 | = 0
| μ 2 3 |
Expand the determinant along the first row:
- (λ+2) * det (| 2 1 |, | μ 3 |) = 0.
- (λ+2) (2*3 - 1*μ) = 0.
(λ+2) (μ-6) = 0.
This implies that either λ+2 = 0 or μ-6 = 0.
So, the conditions are λ = -2 (for any μ) or μ = 6 (for any λ).
New answer posted
4 months agoContributor-Level 10
The general term Tr+1 in the expansion of (a/x + x)^n (assuming from context, as it is not explicitly stated) is:
Tr+1 = nCr * (a/x)^r * x^ (n-r) = nCr * a^r * x^ (n-2r)
(The text shows (a/x^2) leading to x^ (n-3r)
Assuming the term is (x + a/x^2)^n:
Tr+1 = nCr * x^ (n-r) * (a/x^2)^r = nCr * a^r * x^ (n-3r)
T3 = T (2+1) = nC2 * a^2 * x^ (n-6)
T4 = T (3+1) = nC3 * a^3 * x^ (n-9)
T5 = T (4+1) = nC4 * a^4 * x^ (n-12)
The ratio of the coefficients is given:
(nC2 * a^2) / (nC3 * a^3) = 12/8 = 3/2
(n (n-1)/2) * a^2) / (n (n-1) (n-2)/6) * a^3) = 3/2
(3 / (n-2) * (1/a) = 3/2 => a (n-2) = 2 (i)
(nC3 * a^3) / (nC4 * a^4) = 8/3
(n (n-1) (n-2)/6) * a^3)
New answer posted
4 months agoContributor-Level 9
In Hoffmann bromamide reaction, hypobromite ion react with amide and in this reaction carbonyl group is lost as CO? ²? in form of Na? CO?
New answer posted
4 months agoContributor-Level 10
To find the values of a and b, we evaluate the left-hand limit (LHL) and right-hand limit (RHL) at x=0 and equate them.
LHL: lim (x→0) sin (a+3)/2 * x / x = (a+3)/2. The full limit evaluates to (a+3)/2. So, (a+3)/2 = b.
This gives the relation a - 2b + 3 = 0 — (I)
RHL: lim (x→0) [√ (x+bx³) - √x] / (bx²).
Rationalize the numerator:
lim (x→0) [ (x+bx³) - x] / [bx² (√ (x+bx³) + √x)]
= lim (x→0) bx³ / [bx² (√x (√ (1+bx²) + √x)]
= lim (x→0) x / [√x (√ (1+bx²) + 1)] = lim (x→0) √x / (√ (1+bx²) + 1) = 0/2 = 0.
So, b = 0.
Substituting b=0 into equation (I): a - 2 (0) + 3 = 0 ⇒ a = -3.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers