Class 12th

$7^{2022}+3^{2022}$

$={\left(49\right)}^{1011}+{\left(9\right)}^{1011}$

$={\left(50-1\right)}^{1011}+{\left(10-1\right)}^{1011}$

$=5\lambda -1+5k-1$

= 5m – 2

Remainder = 5 – 2 = 3

In DC :-                In AC:-

              i₁ = 4A                 i₂ = 4 sin   $\omega t$

              R₁ = 3   $\Omega$             R₂ =   $2\Omega$

              In same time internal of 't' - $\frac{H_1}{H_2}=\frac{i_1^2{R}_{1}t}{{\left({\mathcal{l}}_{2^{-rms}}\right)}^2{R}_{2}t}=\frac{16*3t}{{\left(\frac{4}{\sqrt[]{2}}\right)}^2*2*t}=\frac{48}{\left(\frac{32}{2}\right)}=3:1$

If y = y(x), $x\in \left(0,\frac{\pi }{2}\right)$ $\frac{}{}$ be the solution curve of the different equation

$\frac{}{}$ $\therefore \frac{dy}{dx}+\left(8+4cot2x\right)y=\frac{2e^{-4x}}{si{n}^{2}2x}\left(2sinx+cos2x\right)$  which is a linear different equation

I.F = $e^{{\displaystyle \int \left(8+4cot2x\right)dx}}=e^{8x+2cos\left(sin2x\right)}=e^{8x}.si{n}^{2}2x$ ${}^{{\displaystyle }}{}^{}{}^{}{}^{}$

Given, $y\left(\frac{\pi }{4}\right)=e^{-\pi }\Rightarrow c=0$ $\frac{}{}{}^{}$

$\therefore y=\frac{e^{-4x}}{sin2x}$

$\therefore y\left(\frac{\pi }{6}\right)=\frac{e^{-4\frac{\pi }{6}}}{sin\left(2.\frac{\pi }{6}\right)}=\frac{2}{\sqrt[]{3}}{e}^{\frac{2\pi }{3}}$

  $\frac{dy}{dx}=\frac{x+y-2}{x-y}$  

Let x – 1 = X, y – 1 = Y

then DE: $\frac{dY}{dX}=\frac{X+Y}{X-Y}=\frac{1+\frac{Y}{X}}{1-\frac{Y}{X}}$  

Put y = vx

then  $\frac{dY}{dX}=V+X\frac{dV}{dX}$  

V + $X\frac{dV}{dX}=\frac{1+V}{1-V}$

$X\frac{dV}{dX}=\frac{1+V}{1-V}-V$

$=\frac{1+V^2}{1-V}$

$\frac{1-V}{1+V^2}dV=\frac{dX}{X}$

$\frac{V-1}{V^2+1}dV+\frac{dX}{X}=0$

$\frac{1}{2}\mathcal{l}n\left|V^2+1\right|-ta{n}^{-1}V+\mathcal{l}n\left|X\right|=c$

$\mathcal{l}n\left(\sqrt[]{1+{\left(\frac{Y-1}{X-}\right)}^2}\cdot \left|X-1\right|\right)ta{n}^{-1}\frac{Y-1}{X-1}=c$

$\left(2,1\right)\Rightarrow \mathcal{l}n\left(\sqrt[]{1+0}\cdot 1\right)-0=c$

c = 0  

$\mathcal{l}n\sqrt[]{{\left(X-1\right)}^2+{\left(Y-1\right)}^2}=ta{n}^{-1}\frac{Y-1}{X-1}$

point (k + 1, 2) $\mathcal{l}n\sqrt[]{k^2+1}=ta{n}^{-1}\frac{1}{k}$

$\Rightarrow \frac{1}{2}\mathcal{l}n\left(k^2+1\right)=ta{n}^{-1}\frac{1}{k}$              

Probability that chosen candidate is female $=\frac{40}{60}=\frac{2}{3}$

I(x) = ${\displaystyle \int \frac{se{c}^{2}x-2022}{si{n}^{2022}x}dx}$  

$={\displaystyle \int si{n}^{-2022}x\cdot se{c}^{2}xdx-{\displaystyle \int 2022si{n}^{-2022}xdx}}$

$=si{n}^{-2022}x\cdot tanx-{\displaystyle \int \left(-2022\right)si{n}^{-2023}x\cdot cosx\cdot tanxdx-{\displaystyle \int 2022si{n}^{-2022}xdx}}$

$=tanx\cdot si{n}^{-2022}x+2022{\displaystyle \int si{n}^{-2022}-2022{\displaystyle \int si{n}^{-2022}xdx}}$

 I(x) = $tanx\cdot si{n}^{-2022}x+c$  

Given,   $I\left(\frac{\pi }{4}\right)=2^{1011}$

-> $2^{1011}=\frac{1}{{\left(\frac{1}{\sqrt[]{2}}\right)}^{2022}}+c\Rightarrow c=0$

$I\left(x\right)=\frac{tanx}{si{n}^{2022}x},I\left(\frac{\pi }{3}\right)=\frac{\sqrt[]{3}}{\left(\frac{\sqrt[]{3}}{2}\right)}=\frac{2^{2022}}{{\left(\sqrt[]{3}\right)}^{2021}}$  

$\left|\overrightarrow{a}\right|=9\&\left(x\overrightarrow{a}+y\overrightarrow{b}\right).\left(6y\overrightarrow{a}-18x\overrightarrow{b}\right)=0$

$\Rightarrow 6xy{\left|\overrightarrow{a}\right|}^2-18x^2\left(\overrightarrow{a}.\overrightarrow{b}\right)+6y^2\left(\overrightarrow{a}.\overrightarrow{b}\right)-18xy{\left|\overrightarrow{b}\right|}^2=0$

This should hold $\forall x,x,y\in R*R$

$\therefore {\left|\overrightarrow{a}\right|}^2=3{\left|\overrightarrow{b}\right|}^2\&\left(\overrightarrow{a}.\overrightarrow{b}\right)=0$

$\therefore \left|\overrightarrow{a}*\overrightarrow{b}\right|=\frac{{\left|\overrightarrow{a}\right|}^2}{\sqrt[]{3}}=\frac{81}{\sqrt[]{3}}=27\sqrt[]{3}$

Let angle of dip =

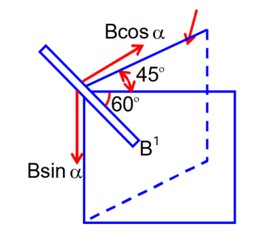
Then B cos 45° = B' cos 60°- (i)

B' sin 60 = B sin - (ii)

$\left(i\right)÷\left(ii\right)\Rightarrow cost60=cot\alpha cos45°$

$cot\alpha =\frac{cot60°}{cos45°}=\frac{1\sqrt[]{2}}{\sqrt[]{3}x}=\sqrt[]{\frac{2}{3}}$

$tan\alpha =\sqrt[]{\frac{3}{2}}$

$\alpha =ta{n}^{-1}\sqrt[]{\frac{3}{2}}$

a₀ = 0, a₁ = 0

a_n+2 = 3a_n+1 – 2a_n + 1

a₂₅ a₂₃ – 2a₂₅a₂₂ – a₂₃a₂₄ + 4a₂₂a₂₄ =?

a₂ = 3a₁ – 2a₀ + 1

a₃ = 3a₂ – 2a₁ + 1

a₄ = 3a₃ – 2a₂ + 1

a₅ = 3a₄ – 2a₃ + 1

a_n+2  = 3a_n+1 – 2a_n + 1

$\left(+\right)\Rightarrow \left(a_2+a_3+a_4+....+a_{n+1}+a_{n+2}\right)$

-> a_n+2 = 2 (a₂ + a₃ + …. + a_n + a_n+1) –2 (a₁ + a₂ + ….+ a_n) + n + 1

a_n+2 = 2a_n+1 + n + 1

a₂₅ a₂₃ -2a₂₅ a₂₂ -a₂₃ a₂₄ + 4a₂₂ a₂₄

= a₂₅ (a₂₃ – 2a₂₂) -2a₂₄ (a₂₃ – 2a₂₂)

As a_n+2 = 2a_n+1 + n + 1

-> a_n+2 – 2a_n+1 = n + 1

-> a_n+1 -2a_n = n

-> 24 * 22 = 528

cos^-1 x = 2 sin^-1 x = cos^-1 2x

$co{s}^{-1}x-2\left(\frac{\pi }{2}-co{s}^{-1}x\right)=co{s}^{-1}2x$          

$cos\left(3co{s}^{-1}x\right)=cos\left(\pi +co{s}^{-1}2x\right)$    

$4x^3-3x=-2x$        

$4x^3=x\Rightarrow x=0\pm \frac{1}{2}$      

All satisfy the original equation

Sum =  $-\frac{1}{2}+0+\frac{1}{2}=0$