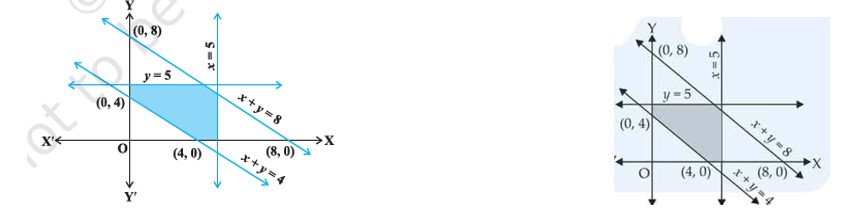- Linear Inequalities Short Answer Type Questions
- Linear Inequalities Long Answer Type Questions
- Linear Inequalities Objective Type Questions
- Linear Inequalities True or False Type Questions
- Linear Inequalities Fill in the blanks Type Questions
- JEE Mains 2020
- JEE Mains 2021
Linear Inequalities Short Answer Type Questions
| 1. Solve: |
| Sol. |
| 2. Solve: |
| Sol. |
Commonly asked questions
A company manufactures cassettes. Its cost and revenue functions are where is the number of cassettes produced and sold in a week? How many cassettes must be sold by the company to realize some profit?
This is a short answer type question as classified in NCERT Exemplar
The water acidity in a pool is considered normal when the average pH reading of three daily measurements is between 8.2 and 8.5. If the first two pH readings are and , find the range of pH values for the third reading that will result in the acidity level being normal.
This is a short answer type question as classified in NCERT Exemplar
A solution of 9% acid is to be diluted by adding 3% acid solution to it. The resulting mixture is to be more than 5% but less than 7% acid. If there are 460 liters of the 9% solution, how many liters of the 3% solution will have to be added?
This is a short answer type question as classified in NCERT Exemplar
A solution is to be kept between and . What is the range of temperature in degrees Fahrenheit if the conversion formula is
This is a short answer type question as classified in NCERT Exemplar
Solve:
This is a short answer type question as classified in NCERT Exemplar
Solve:
This is a short answer type question as classified in NCERT Exemplar
Solve:
This is a short answer type question as classified in NCERT Exemplar
Solve:
This is a short answer type question as classified in NCERT Exemplar
Solve:
This is a short answer type question as classified in NCERT Exemplar
Solve:
This is a short answer type question as classified in NCERT Exemplar
The longest side of a triangle is twice the shortest side, and the third side is 2 longer than the shortest side. If the perimeter of the triangle is more than 166, then find the minimum length of the shortest side.
This is a short answer type question as classified in NCERT Exemplar
In drilling the world’s deepest hole, it was found that the temperature T in degrees Celsius, x below the earth’s surface, was given by At what depth will the temperature be between and ?
This is a short answer type question as classified in NCERT Exemplar
Linear Inequalities Long Answer Type Questions
| 1. Solve the following system of inequalities: |
| Sol. |
| 2. Find the linear inequalities for which the shaded region in the given figure is the solution set. |
| Sol. Sol. |
Commonly asked questions
Solve the following system of inequalities:
This is a long answer type question as classified in NCERT Exemplar
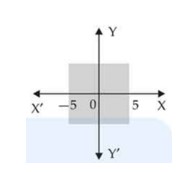
Find the linear inequalities for which the shaded region in the given figure is the solution set.
This is a long answer type question as classified in NCERT Exemplar
Find the linear inequalities for which the shaded region in the given figure is the solution set.
This is a long answer type question as classified in NCERT Exemplar
Show that the following system of linear inequalities has no solution:
This is a long answer type question as classified in NCERT Exemplar
Linear Inequalities Objective Type Questions
| 1. If , then (a) (b) (c) (d) |
| Sol. |
| 2. Given that and are real numbers and , then (a) (b) (c) (d) |
| Sol. |
Commonly asked questions
If , then
(a)
(b)
(c)
(d)
This is an Objective Type Questions as classified in NCERT Exemplar
Given that and are real numbers and , then
(a)
(b)
(c)
(d)
This is an Objective Type Questions as classified in NCERT Exemplar
If is a real number and , then
(a)
(b)
(c)
(d)
This is an Objective Type Questions as classified in NCERT Exemplar
Choose the correct option for :
(a)
(b)
(c)
(d)
This is an Objective Type Questions as classified in NCERT Exemplar
Choose the correct option for :
(a)
(b)
(c)
(d)
This is an Objective Type Questions as classified in NCERT Exemplar
If , then
(a)
(b)
(c)
(d)
This is an Objective Type Questions as classified in NCERT Exemplar
If and , then
(a)
(b)
(c)
(d)
This is an Objective Type Questions as classified in NCERT Exemplar
If , then
(a)
(b)
(c)
(d)
This is an Objective Type Questions as classified in NCERT Exemplar
If , then
(a)
(b)
(c)
(d)
This is an Objective Type Questions as classified in NCERT Exemplar
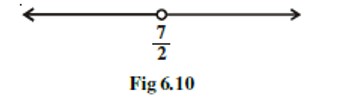
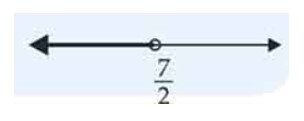
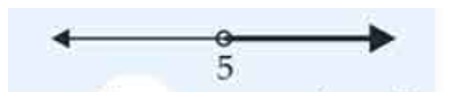
The inequality representing the following graph is:
Fig. 6.7
(a)
(b)
(c)
(d)
This is an Objective Type Questions as classified in NCERT Exemplar
Choose the correct option for :
(a)
(b)
(c)
(d)
This is an Objective Type Questions as classified in NCERT Exemplar
Choose the correct option for :
(a)
(b)
(c)
(d)
This is an Objective Type Questions as classified in NCERT Exemplar
Linear Inequalities True or False Type Questions
zzzzzzzz
Commonly asked questions
(i) If and , then
(ii) If , then and .
(iii) If , then and .
(iv) If , then and .
(v) If and , then .
(vi) If and , then .
(vii) If and , then .
(viii) If , then
(ix) If , then
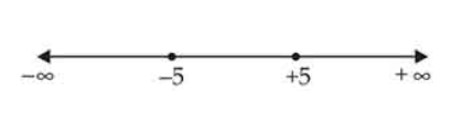
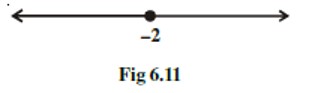
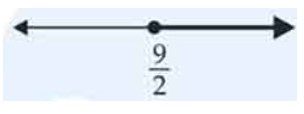
(x) Graph of corresponds to Fig 6.12.
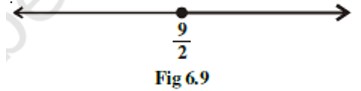
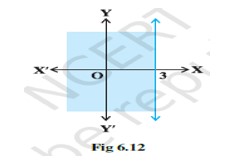
(xi) Graph of corresponds to Fig 6.13.
(xii) Graph of corresponds to Fig 6.14.
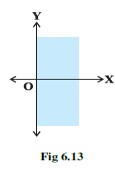
(xiii) Solution set of and corresponds to Fig 6.15.
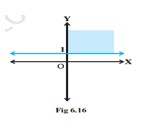
(xiv) Solution set of and corresponds to Fig 6.16.
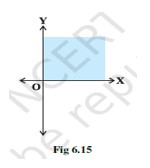
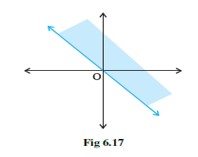
(xv) Solution set of corresponds to Fig 6.17.
This is a True or False Type Questions as classified in NCERT Exemplar
Linear Inequalities Fill in the blanks Type Questions
qqqqqqqqqqq
Commonly asked questions
(i) If , then .
(ii) If then .
(iii) If then .
(iv) If , then .
(v) If and , then .
(vi) If and , then .
(vii) If , then or .
(viii)If , then .
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
JEE Mains 2020
JEE Mains 2020
Commonly asked questions
If the letters of the word 'MOTHER' be permuted and all the words so formed (with or without meaning) be listed as in a dictionary, then the position of the word 'MOTHER' is.
MOTHER
1? E
2? H
3? M
4? O
5? R
6? T
So position of word MOTHER in dictionary
2*5!+2*4!+3*3!+2!+1
=240+48+18+2+1
=309
Let a, b and c be three unit vectors such that |a-b|²+|a-c|²=8. Then |a+2b|²+|a+2c|² is equal to.
|a|=|b|=|c|=1
|a-b|²+|a-c|²=8
⇒|a|²+|b|²-2a.b+|a|²+|c|²-2a.c=8
⇒4-2 (a.b+a.c)=8
⇒a.b+a.c=-2
|a+2b|²+|a+2c|²
=|a|²+4|b|²+4a.b+|a|²+4|c|²+4a.c
=10+4 (a.b+a.c)
=10-8=2
If lim(x→1) (x+x²+x³+...+xⁿ-n)/(x-1) = 820, (n∈N) then the value of n is equal to.
lim (x→1) (x+x²+.+x? -n)/ (x-1) = 820
⇒ lim (x→1) (x-1)/ (x-1)+ (x²-1)/ (x-1)+.+ (x? -1)/ (x-1) = 820
⇒ 1+2+.+n = 820
⇒ n (n+1)=2×820
⇒ n (n+1)=40×41
Since n∈N, so n=40
The number of integral values of k for which the line, 3x+4y=k intersects the circle, x²+y²-2x-4y+4=0 at two distinct points is.
Circle x²+y²-2x-4y+4=0
⇒ (x-1)²+ (y-2)²=1
Centre: (1,2) radius=1
line 3x+4y-k=0 intersects the circle at two distinct points.
⇒ distance of centre from the line < radius
⇒ |3×1+4×2-k|/√ (3²+4²) < 1
⇒ |11-k|<5
⇒ 6
Number of K is 9.
The integral ∫₀² ||x-1|-x|dx is equal to [numerical value].1|-x|dx is equal to.
∫? ² |x-1|-x|dx
Let f (x)=|x-1|-x|
= {|1-2x|, x≤1; 1, x≥1}
A = 1/2+1=3/2
∫? ¹/² (1-2x)dx+∫? /? ¹ (2x-1)+∫? ²1dx
= [x-x²]? ¹/²+ [x]? ² = 3/21dx
= [x-x²]? ¹/²+ [x]? ² = 3/2
JEE Mains 2021
JEE Mains 2021
Commonly asked questions
If f(x) = ∫ [5x⁸ + 7x⁶] / [(x⁷ + x² + 1)²] dx, (x > 0), f(0) = 0 and f(1) = 1/K, then the value of K is ______.
f (x) = ∫ (5x? + 7x? ) / (x² + 1 + 2x? ) dx seems to have a typo in the denominator. Based on the solution, the denominator is (x? + 1/x? + 2)² or similar. Let's follow the solution's steps.
It seems the denominator is (x? (2 + 1/x? + 1/x? )² = x¹? (2 + 1/x? + 1/x? )².
f (x) = ∫ (5x? + 7x? ) / (x¹? (2 + 1/x? + 1/x? )²) dx
The solution simplifies the integrand to:
f (x) = ∫ (5/x? + 7/x? ) / (2 + 1/x? + 1/x? )² dx
Let t = 2 + 1/x? + 1/x?
dt = (-5/x? - 7/x? ) dx = - (5/x? + 7/x? ) dx.
The integral becomes:
f (x) = ∫ -dt / t² = 1/t + C.
f (x) = 1 / (2 + 1/x? + 1/x? ) + C.
Given f (0)=0, this form has a division by zero. Let's re-examine the original problem. If x≥0, as x→0, the integrand goes to 0. So f (0)=0 implies C=0. Let's assume the function is defined as the limit.
However, f (x) = x? / (2x? + x² + 1) + C is a more likely result.
Given f (1) = 1/k:
f (1) = 1 / (2 + 1 + 1) = 1/4.
So, 1/k = 1/4 => k = 4.
The mean age of 25 teachers in a school is 40 years. A teacher retires at the age of 60 years and a new teacher is appointed in his place. If the mean age of the teachers in this school now is 39 years, then the age (in years) of the newly appointed teacher is: ______.
Initial mean of 25 observations is 40.
X? = (Σx? )/25 = 40 => Σx? = 25 * 40 = 1000.
A teacher of age 60 retires.
The new sum of ages for the remaining 24 people is 1000 - 60 = 940.
A new teacher of age x joins.
The new sum for 25 people is 940 + x.
The new mean is 39.
(940 + x) / 25 = 39
940 + x = 39 * 25 = 975
x = 975 - 940 = 35.
The new teacher's age is 35.
The missing value in the following figure is ______. (A diagram with numbers in a circular pattern is shown).
1 = (2-1)¹ (The n is likely 1).
3? = (7-4)³ (This seems to be a pattern matching (a-b)^c).
4²? = (12-8)? ! = 4²?
The blank space must be (5-3)² = 2² = 4.
The equation of the planes parallel to the plane x - 2y + 2z - 3 = 0 which are at unit distance from the point (1,2,3) is ax + by + cz + d = 0. If (b-d) = K(c-a), then the positive value of K is ______.
The equation of a plane parallel to x - 2y + 2z - 3 = 0 is x - 2y + 2z + λ = 0.
The distance from the point (1, 2, 3) to this plane is 1.
|1 - 2 (2) + 2 (3) + λ| / √ (1² + (-2)² + 2²) = 1
|1 - 4 + 6 + λ| / √9 = 1
|3 + λ| / 3 = 1
|3 + λ| = 3
3 + λ = 3 or 3 + λ = -3
λ = 0 or λ = -6.
Maths NCERT Exemplar Solutions Class 11th Chapter Six Exam