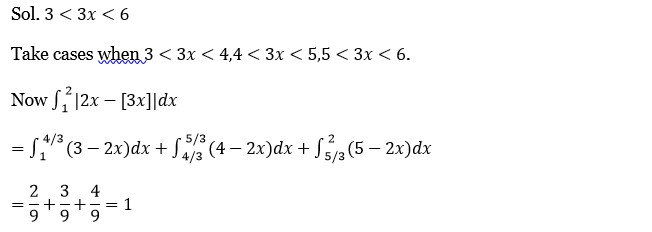Maths Integrals

I = ∫sin? ¹ (√x/√1+x)dx
∫tan? ¹ (√x)dx
= xtan? ¹√x - ∫ (1/ (1+x) * 1/ (2√x)xdx + C

= xtan? ¹√x - ∫ (t²/ (1+t²) * (t*2t dt)/ (2t) + C (x=t²)
= xtan? ¹√x - ∫ (t²/ (1+t²)dt + C = xtan? ¹√x - t + tan? ¹t + C = xtan? ¹√x - √x + tan? ¹√x + C
= (x+1)tan? ¹√x - √x + C => (Ax) = x+1 => B (x) = -√x

k/6 = ∫? ^ (π/6) (x²)/ (1-x²)³/² dx x = sinθ dx = cosθdθ
=> k/6 = ∫? ^ (π/6) (sin²θ)/ (1-sin²θ)³/² * cosθdθ
=> k/6 = ∫? ^ (π/6) (sin²θ)/ (cos³θ) * cosθdθ
=> k/6 = ∫? ^ (π/6) tan²θdθ = ∫? ^ (π/6) (sec²θ-1)dθ
=> k/6 = [tanθ - θ]? ^ (π/6) = (1/√3 - π/6) = (2√3-π)/6
=> k = 2√3 - π

Below are a few important tips to remember the integrals of some particular functions:
1. Know the derivatives for each integral.
2. Make yourself familiar with the standard formulas first.
3. Practice daily for better memory.
4. Group similar formulas

Students can find the formula of integration for a particular function in this article. It is important to memorise these formulas to solve the integral problem easily. Below is the integration of a particular function formula.

The formula of a particular function:

1. Power Rule: 

$\int x^{n}dx=\frac{x^{n+1}}{n+1}+C(n\ne -1)$

2. Reciprocal Function:

$\int \frac{1}{x}dx=ln\left|x\right|+C$

3. Trigonometric Function: 

• $\int sinxdx=-cosx+C$
• $\int cosxdx=sinx+C$
• $\int {sec}^{2}xdx=tanx+C$
• $\int {csc}^{2}xdx=-cotx+C$
• $\int secxtanxdx=secx+C$
• $\int cscxcotxdx=-cscx+C$

4. Inverse Trigonometric Function

• $\int \frac{1}{1+x^2}dx={tan}^{-1}x+C$
• $\int \frac{1}{\sqrt{1-x^2}}dx={sin}^{-1}x+C$
• $\int \frac{-1}{\sqrt{1-x^2}}dx={cos}^{-1}x+C$

∫ [-π to π] |π - |x|dx = 2∫ [0 to π] |π - x|dx
= 2∫ [0 to π] (π - x)dx
= 2 [πx - x²/2] (from 0 to π) = π²