Maths NCERT Exemplar Solutions Class 11th Chapter Two
Get insights from 107 questions on Maths NCERT Exemplar Solutions Class 11th Chapter Two, answered by students, alumni, and experts. You may also ask and answer any question you like about Maths NCERT Exemplar Solutions Class 11th Chapter Two
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
3 months agoContributor-Level 9
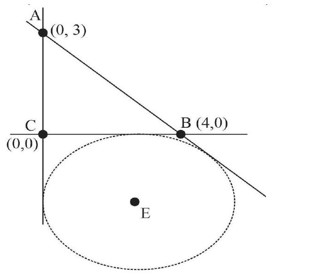
Equation of normal must pass through centre
point of contact of normal at parabola is
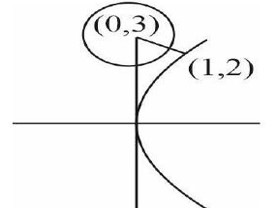
So distance between parabola and circle is
New answer posted
3 months agoContributor-Level 9
Equation of any plane passing through the line of intersection of planes (1) and (2)
If (3) & (4) is same plane.
(i)
(ii) (iii)
By (i) & (ii)
By (ii) & (iii)
New answer posted
3 months agoContributor-Level 9
Magnitude of all vectors will be same as well as angle between these vectors will also be same.
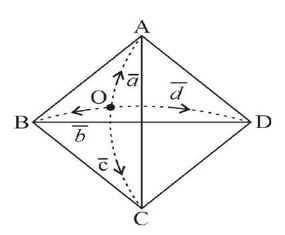
New answer posted
3 months agoContributor-Level 9
Case-I:
Case-II:
By solving (1) & (2)
Equation (4) has no solution
.(5) By equation (5) .
We obtain solving equation (2)
or
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 680k Reviews
- 1800k Answers