Maths

cos^-1 x = 2 sin^-1 x = cos^-1 2x

$co{s}^{-1}x-2\left(\frac{\pi }{2}-co{s}^{-1}x\right)=co{s}^{-1}2x$          

$cos\left(3co{s}^{-1}x\right)=cos\left(\pi +co{s}^{-1}2x\right)$    

$4x^3-3x=-2x$        

$4x^3=x\Rightarrow x=0\pm \frac{1}{2}$      

All satisfy the original equation

Sum =  $-\frac{1}{2}+0+\frac{1}{2}=0$

y = 2x - $\left|3x^2-5x+2\right|,0\le x\le 1$  

$=\{\begin{array}{cc}\hfill -3x^2+7x-2,\hfill & \hfill 3x^2-3x+2,\hfill \end{array}\begin{array}{cc}\hfill 0\le x\le \frac{2}{3}\hfill & \hfill \frac{2}{3}<x\le 1\hfill \end{array}$               

 3x² – 5x + 2 = 0

$x=\frac{+5\pm \sqrt[]{25-24}}{6}$               

= $\frac{5+1}{6}=1,\frac{2}{3}$

3x² – 7x + 3 = 0

x = $\frac{7\pm \sqrt[]{49-39}}{6}=\frac{7\pm \sqrt[]{13}}{6}$

$-3x^2+7x-2$

$\frac{-7\pm \sqrt[]{49-24}}{-6}=\frac{7+5}{6}=2,\frac{1}{3}$  

3x² + 7x – 2 = -1

->3x² – 7x + 1 = 0

x =   $\frac{7\pm \sqrt[]{49-12}}{6}=\frac{7\pm \sqrt[]{37}}{6}$

I =   ${\displaystyle \underset{0}{\overset{6}{\int }}\left(\begin{array}{cc}\hfill \left(-2\right)\hfill & \hfill +1\hfill \end{array}\right)dx+{\displaystyle \underset{\frac{7-\sqrt[]{37}}{6}}{\overset{\frac{1}{3}}{\int }}\left(\begin{array}{cc}\hfill \left(-1\right)\hfill & \hfill +1\hfill \end{array}\right)dx}+{\displaystyle \underset{-\frac{1}{3}}{\overset{\frac{7-\sqrt[]{13}}{6}}{\int }}\left(\begin{array}{cc}\hfill 0\hfill & \hfill +1\hfill \end{array}\right)dx+{\displaystyle \underset{\frac{7-\sqrt[]{13}}{6}}{\overset{\frac{2}{3}}{\int }}\left(1+1\right)dx}}}+{\displaystyle \underset{\frac{2}{3}}{\overset{1}{\int }}\left(1+1\right)dx}$

$=\frac{\sqrt[]{37}+\sqrt[]{13}-4}{6}$

By its given condition

$\stackrel{}{}\stackrel{}{}\stackrel{}{}$  $\therefore \overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ are linearly independent vectors is $\left[\overrightarrow{a}\overrightarrow{b}\overrightarrow{c}\right]\ne 0$ $\stackrel{}{}\stackrel{}{}\stackrel{}{}$

Now, $\left[\overrightarrow{a}\overrightarrow{b}\overrightarrow{c}\right]$ $\stackrel{}{}\stackrel{}{}\stackrel{}{}$ = $\left|\begin{array}{ccc}\hfill 1+t\hfill & \hfill 1-t\hfill & \hfill 1\hfill \\ \hfill 1-t\hfill & \hfill 1+t\hfill & \hfill 2\hfill \\ \hfill t\hfill & \hfill -t\hfill & \hfill 1\hfill \end{array}\right|\ne 0$ $\begin{array}{ccc}\hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}$

$R_1-R_2,R_2+R_3$

$R_1-R_2\Rightarrow \left|\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill -3\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 3\hfill \\ \hfill t\hfill & \hfill -t\hfill & \hfill \mathcal{l}\hfill \end{array}\right|\ne 0\Rightarrow t\ne 0$

$\left|\frac{x^2+4x+2}{x^2+3}\right|\le 1$

${\left(x^2-4x+2\right)}^2\le {\left(x^2+3\right)}^2$

$\Rightarrow \left(2x^2-4x+5\right)\left(-4x-1\right)\le 0$

$\Rightarrow -4x-1\le 0\to x\ge -\frac{1}{4}$

$\underset{x?0}{lim}\frac{\mathcal{l}n\frac{1+5x}{1+?x}}{x}=10$

$\underset{x?0}{lim}\mathcal{l}n\left\{\frac{1+\left(5??\right)x}{\frac{\left(5??\right)x}{1+?x}?\left(\frac{1+?x}{5??}\right)}\right\}$

5 = 10

= 5

$xdy=\left(\sqrt[]{x^2+y^2}+y\right)dx$

$\frac{xdy-ydx}{x^2}=\sqrt[]{1+\frac{y^2}{x^2}}dx$

$\frac{d\left(\frac{y}{x}\right)}{\sqrt[]{1+{\left(\frac{y}{x}\right)}^2}}=\frac{dx}{x}\Rightarrow \mathcal{l}n\left(\frac{y}{x}+\sqrt[]{{\left(\frac{y}{x}\right)}^2+1}\right)=\mathcal{l}nx+C$

$\alpha =\frac{3}{2}$

$\Delta =0$

$\left|\begin{array}{ccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 2\hfill & \hfill 5\hfill & \hfill \alpha \hfill \\ \hfill 1\hfill & \hfill 2\hfill & \hfill 3\hfill \end{array}\right|=0$

15 - 2a + a - 6 – 1 = 0

a = 8

For a = 8, equations are

x + y + 3 = 6

2x + 5y + 8z = b

x + 2y + 3z = 14

$\left(2,5,8\right)=\mathcal{l}\left(1,1,1\right)+m\left(1,2,3\right)$

$\begin{array}{cc}\hfill 2=\mathcal{l}+m\hfill & \hfill 5=\mathcal{l}+2m\hfill \end{array}]\to 3=m,\mathcal{l}=-1$              

8 =  $\mathcal{l}+3m$

$\beta =6\mathcal{l}+14m$

= -6 + 42 = 36

a + b = 8 + 36 = 44

$A=\left[\begin{array}{cc}\hfill -1\hfill & \hfill 2\hfill \\ \hfill 1\hfill & \hfill -1\hfill \end{array}\right]$

$EA=\left[\begin{array}{cc}\hfill a\hfill & \hfill c\hfill \\ \hfill b\hfill & \hfill d\hfill \end{array}\right]\left[\begin{array}{cc}\hfill -1\hfill & \hfill 2\hfill \\ \hfill 1\hfill & \hfill -1\hfill \end{array}\right]$

$=\left[\begin{array}{cc}\hfill -a+c\hfill & \hfill 2a-c\hfill \\ \hfill -b+d\hfill & \hfill 2b-d\hfill \end{array}\right]$

For a = c For $\begin{array}{cc}\hfill -a+c=0\hfill & \hfill 2a-c=1\hfill \end{array}]\to a=1,c=1E=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$  

d = b + 1, d = 1, b = 0

$\begin{array}{cc}\hfill b+d=1\hfill & \hfill 2b-d=-1\hfill \end{array}]\to b=0,d=1R_1\to R_1\to R_2\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$

For  $\begin{array}{cc}\hfill -a+c=1\hfill & \hfill 2a-c=1\hfill \end{array}]\to a=0,c=1$

$For\begin{array}{cc}\hfill -a+c=-1\hfill & \hfill 2a-c=2\hfill \end{array}]\to a=1,c=0$

$\begin{array}{cc}\hfill -b+d=-2\hfill & \hfill 2b-d=7\hfill \end{array}]\to b=5,d=3\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 5\hfill & \hfill 3\hfill \end{array}\right]\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$

R₂ -> 5R₁ + 3R₂

For $For\begin{array}{cc}\hfill -a+c=-1\hfill & \hfill 2a-c=2\hfill \end{array}]\to a=1,c=1$

$\begin{array}{cc}\hfill -b+d=-1\hfill & \hfill 2b-d=3\hfill \end{array}]\to b=2,d=1$

(A) ® R₁ ® R₁ + R₂

_{(B) ® R2 ® R2 + 2R1 $\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 2\hfill & \hfill 1\hfill \end{array}\right]\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$}

(C) ® R₂ ® 3R₂ + 5R₁

$\left|z-\frac{1}{z}\right|=2$

${\left|z\right|}_{max}=?$

$\left|z-\frac{1}{2}\right|\ge \left|\left|z\right|-\frac{1}{\left|z\right|}\right|$

$2\ge \left|r-\frac{1}{r}\right|$

0 $\le r^2+2r-1\&r^2-2r-1\le 0$

$r=\frac{-2\pm \sqrt[]{8}}{2}$ $r=\frac{2\pm \sqrt[]{8}}{2}$

$=-1\pm \sqrt[]{2}$ $=1\pm \sqrt[]{2}$

r $\ge \sqrt[]{2}-1\&0\le r\le 1+\sqrt[]{2}$

$\sqrt[]{2}-1\le r\le \sqrt[]{2}+1$

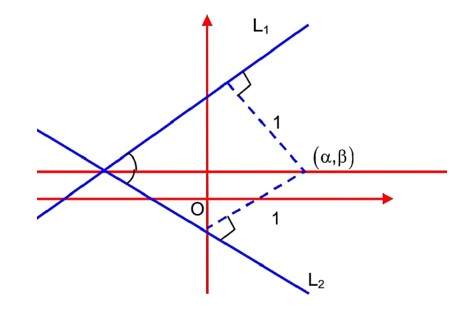
L₁ : 3x – 4y + 12 = 0

L₂ : 8x + 6y + 11 = 0

$\left(\alpha ,\beta \right)$ lies on that angle which contain origin

$\therefore$ Equation of angle bisector of that angle which contain origin is

$\frac{3x-4y+12}{5}=\frac{8x+6y+11}{10}$

$\Rightarrow 2x+14y-13=0$

$\left(\alpha ,\beta \right)$ lies on it

$\Rightarrow 2\alpha +14\beta -13=0$ …… (i)

$\Rightarrow 3\alpha -4\beta +7=0$ ……. (ii)

Solving (i) & (ii)

$\alpha =-\frac{23}{25}\&\beta =\frac{53}{50}$

$\therefore \alpha +\beta =\frac{7}{50}$

$\Rightarrow 100\left(\alpha +\beta \right)=14$