Maths

The shortest distance between the lines $\frac{x + 7}{- 6} = \frac{y - 6}{7} = Z a n d \frac{7 - x}{2} = y - 2 = z - 6$ is

0 Follower 3 Views

Contributor-Level 10

$A (- 7 \hat{i} + 6 \hat{j}) C (7 \hat{i} + 2 \hat{j} + 6 \hat{k})$

$\vec{b} = - 6 \hat{i} + 7 \hat{j} + \hat{k}$ $\vec{d} = - 2 \hat{i} + \hat{j} + \hat{k}$

$\vec{b} * \vec{d} = | \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ - 6 & 7 & 1 \\ - 2 & 1 & 1 \end{matrix} | = 3 \hat{i} + 2 \hat{j} + 4 \hat{k}$

the shortest distance between the lines

$=$ $| \frac{42 - 8 + 24}{29} |$ $=$ $\frac{58}{29}$ $=$ $2$

0 0

New answer posted

3 months ago

A plane E is perpendicular to the two planes 2x – 2y + z = 0 and x – y + 2z = 4, and passes through the point P(1, -1, 1). If the distance of the plane E from the point Q(a, a, 2) is $3 \sqrt[]{2},$ then (PQ)² is equal to

0 Follower 3 Views

Contributor-Level 10

First plane, P₁ = 2x – 2y + z = 0,

normal vector $\equiv n_{1} = (2, - 2, 1)$

Second plane, P₂ = x – y + 2z = 4,

normal vector $\equiv n_{2} = (1, - 1, 2)$

Plane perpendicular to P₁ and P₂ will have normal vector n₃ where n₃ = (n₁* n₂)

Hence,

n₃ = (3, 0)

Distance PQ

$= \sqrt[]{21} \Rightarrow {(P Q)}^{2} = 21$

0 0

New answer posted

3 months ago

Maths Class 11th

Let the foci of the ellipse $\frac{x^{2}}{16} + \frac{y^{2}}{7} = 1$ and the hyperbola $\frac{x^{2}}{144} - \frac{y^{2}}{α} = \frac{1}{25}$ coincide. Then the length of the latus rectum of the hyperbola is

0 Follower 3 Views

Contributor-Level 10

Ellipse : $\frac{x^{2}}{16} + \frac{y^{2}}{7} = 1$

Eccentricity = $\sqrt[]{1 - \frac{7}{10}} = \frac{3}{4}$

Foci $\equiv (\pm a e, 0)$ $\equiv (\pm 3, 0)$

Hyperbola : $\frac{x^{2}}{(\frac{144}{25})} - \frac{y^{2}}{(\frac{α}{25})} = 1$

Eccentricity = $\sqrt[]{1 + \frac{α}{144}} = \frac{1}{12} \sqrt[]{144 + α}$

$= 2 . \frac{\frac{81}{25}}{\frac{12}{5}} = \frac{27}{10}$

0 0

New answer posted

3 months ago

Maths Class 11th

The tangents at the points A(1, 3) and B(1, -1) on the parabola y² – 2x – 2y = 1 meet at the point P. Then the area (in unit²) of the triangle PAB is

0 Follower 2 Views

Contributor-Level 10

$y^{2} - 2 x - 2 y = 1$

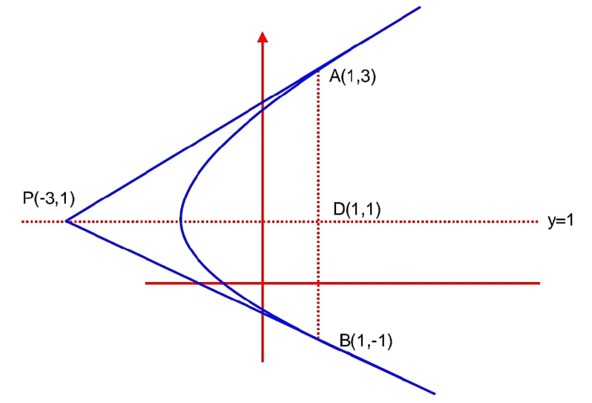
$\Rightarrow {(y - 1)}^{2} = 2 (x + 1)$ …. (i)

Equation of tangent at A is 2x – y – 5 = 0 ………. (ii)

D is mid point of AB solving (ii) with y = 1 P (3, 1)

$∴ P D = 4, A D = 2$

$A r e a o f Δ A P D = \frac{1}{2} (P D) (A D) = 4$

$∴ A r e a o f Δ A P B = 8 s q . u n i t s$

0 0

New answer posted

3 months ago

Maths Class 11th

The statement $(p \Rightarrow q) \lor (p \Rightarrow r)$ is NOT equivalent to

0 Follower 2 Views

Contributor-Level 10

$(A) \sim (p \land (\sim r)) \lor q = (\sim p) \lor (r) \lor q$

(B) $q \lor (- r \lor p)$

(C) $(\sim p) \lor (q \lor r)$

(D) $(\sim p \lor q) \lor r$

Using Venn diagram we get B as the correct option.

0 0

New answer posted

3 months ago

The domain of the function f(x) = $s i n^{- 1} (\frac{x^{2} - 3 x + 2}{x^{2} + 2 x + 7}) i s :$

0 Follower 2 Views

Contributor-Level 10

$- 1 \leq \frac{x^{2} - 3 x + 2}{x^{2} + 2 x + 7} \leq 1$

$\Rightarrow 0 \leq \frac{2 x^{2} - x + 9}{x^{2} + 2 x + 7} & \frac{- 5 x - 5}{x^{2} + 2 x + 7} \leq 0$

$x \in R & - 1 \leq x < \infty$

0 0

New answer posted

3 months ago

Let $\vec{a}, \vec{b}, \vec{c}$ be three coplanar concurrent vectors such that angles between any two of them is same. If the product of their magnitudes is 14 and $(\vec{a} * \vec{b}) . (\vec{b} * \vec{c}) + (\vec{b} * \vec{c}) . (\vec{c} * \vec{a}) + (\vec{c} * \vec{a}) . (\vec{a} * \vec{b})$ = 168, then $| \vec{a} | + | \vec{b} | + | \vec{c} |$ is equal to:

0 Follower 2 Views

Contributor-Level 10

Given : $\hat{a} \cdot \hat{b} = \hat{b} \cdot \hat{c} = \hat{c} \cdot \hat{a} = c o s θ (s a y)$

$| \vec{a} | | \vec{b} | | \vec{c} | = 14$

$(\vec{a} * \vec{b}) \cdot (\vec{b} * \vec{c})$

$= \vec{a} \cdot [(\vec{b} \cdot \vec{c}) \vec{b} - (\vec{b} \cdot \vec{b}) \vec{c}]$

$= (\vec{a} \cdot \vec{b}) (\vec{b} \cdot \vec{c}) - {| \vec{b} |}^{2} \vec{a} \cdot \vec{c}$

$= | \vec{a} | {| \vec{b} |}^{2} | \vec{c} | (c o s^{2} θ - c o s θ) = 14 | \vec{b} | (c o s^{2} θ - c o s θ)$

Similarly, $(\vec{b} * \vec{c}) \cdot (\vec{c} * \vec{a})$

= $| \vec{b} | {| \vec{c} |}^{2} | \vec{a} | (c o s^{2} θ - s i n θ) = 14 | \vec{c} | (c o s 2 θ - s i n θ) & (\vec{c} * \vec{a}) \cdot (\vec{a} * \vec{b})$

$= | \vec{c} | {| \vec{a} |}^{2} | \vec{b} | (c o s^{2} θ - s i n θ) = 14 | \vec{a} | (c o s^{2} θ - s i n θ)$

Given : 14 $(c o s^{2} θ - c o s θ) (| \vec{a} | + | \vec{b} | + | \vec{c} |) = 168$

$| \vec{a} | + | \vec{b} | + | \vec{c} | = \frac{12}{c o s^{2} θ - c o s θ} = \frac{12}{\frac{1}{4} - (- \frac{1}{2})} = \frac{12}{\frac{3}{4}} = 16$

Given : $\vec{a}, \vec{b}, \vec{c}$ are coplanar & pair wise equal angle.

0 0

New answer posted

3 months ago

Let $S = {z = x + i y | z - 1 + i | \geq | z |, | z | < 2, | z + i | = | z - 1 |} .$ Then the set of all values of x, for which $w = 2 x + i y \in S$ for some $y \in R,$ is

0 Follower 2 Views

Contributor-Level 10

$| z - 1 + i | \geq | z |$

$| z + i | = | z - 1 |$

W = (2x, y) = (a, y)

Let S represent the line segment AB

For 'B'

x² + y² = 4

x = -y

-> x² = 2

$x = \pm \sqrt[]{2}$

-> $B (- \sqrt[]{2}, \sqrt[]{2})$

$A (\frac{1}{2}, - \frac{1}{2})$

W (2x, y) lies on AB

-> $- \sqrt[]{2} < 2 x \leq \frac{1}{2}$

$(| z | < 2)$

$- \frac{1}{\sqrt[]{2}} < x \leq \frac{1}{4}$

0 0

New answer posted

3 months ago

Bag I contains 3 red, 4 black and 3 white balls and Bag II contains 2 red, 5 black and 2 white balls. One ball is transferred from Bag I to Bag II and then a ball is drawn from Bag II. The balls so drawn is found to be black in colour. Then the probability, that the transferred ball is red, is:

0 Follower 4 Views