Maths
Get insights from 6.5k questions on Maths, answered by students, alumni, and experts. You may also ask and answer any question you like about Maths
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
6 months agoContributor-Level 10
The given equation of the curve is --------(1)
and that of the line is ---------(2)
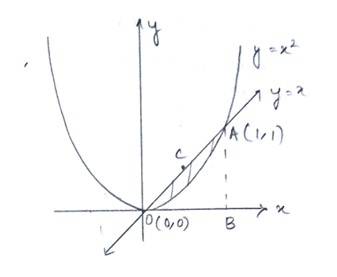
Solving eq (1) and (2)for x and y
Where,
And when
The point of intersection of the parabola and the line
Is O(0,0) and B (1,1)
Hence, area between the curve and the line is
New answer posted
6 months agoContributor-Level 10
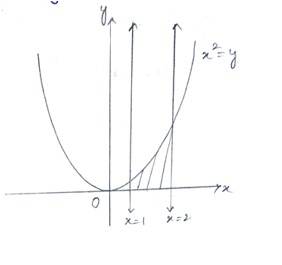
(i) Given of curve is and the equation are
Area enclosed
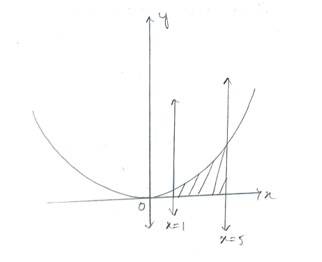
(ii) Given equation of curve is and the lines are
So, area enclosed
New answer posted
6 months agoContributor-Level 10
The given equation of the curve is - (1) and
the line is - (2)
Solving (1) and (2) for x and y
So,
for we get
for , we get
so, the point of intersection are (0,0)and (1,2)
area (DCAO)=area (DCABO)-area ( )
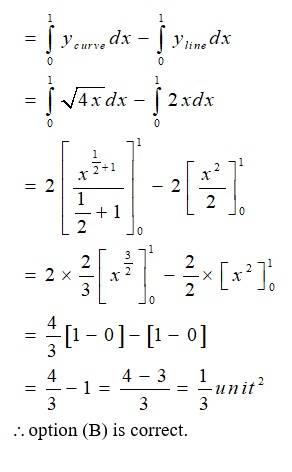
New answer posted
6 months agoContributor-Level 10
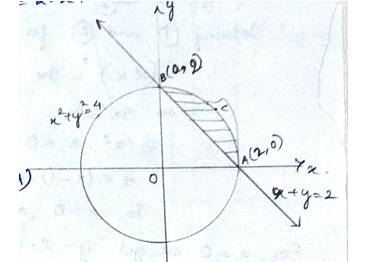
The equation of circle is which has centre at (0,0) & radius,
And the line
The smaller area of circle is given by
Area (ABCA) area (BOAB) – area (BOA)

New answer posted
6 months agoContributor-Level 10
The given equation of the sides of triangle is
--------------------(1)
-------------------(2)
-------------------------(3)
Solving eqn (1) and (2) for x & y we get
The point of inersection of line (1)and (2)is A (0,1)
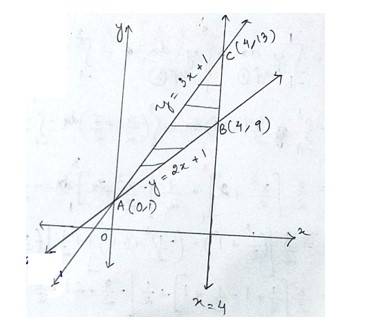
Putting x=4 in eq (1) and (2)we get,
The point of intersection of line (1)and (3) is B(4,9) and C (4,13)
Hence the required area enclosed ABC
New answer posted
6 months agoContributor-Level 10
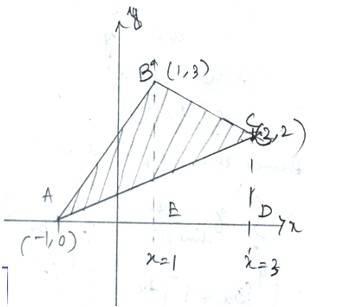
Let A (-1,0),B(1,3) and C (3,2) be the vertices of a triangle ABC
So, equation of line AB is
-------------(1)
Equation of line BC is
---------------(2)
Equation of line AC is
------------------------------(3)
Area of ABC= area ( )
New answer posted
6 months agoContributor-Level 10
The equation of the curve is - (1) and
lines are
- (2)
- (3)
- (4)
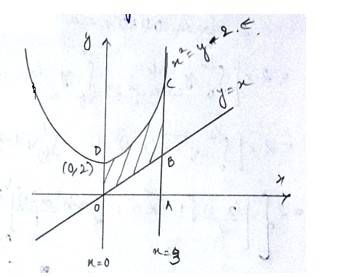
Equation (1)is a parabola with vertex (0,2)
Equation (2)is a straight line passing origin with shape =
The required area enclosed OBCDO = area (ODCAO)-area (OBAO)
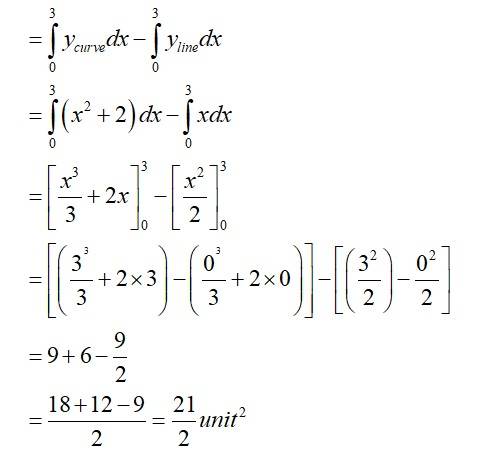
New answer posted
6 months agoContributor-Level 10
The equation of the given circle is
- (1)
- (1) - (2)
Equation (1) is a circle with centre 0 (0,0) and radius 1. Equation (2) is a circle with centre c (1,0) and radius 1.
Solving (1) and (2)
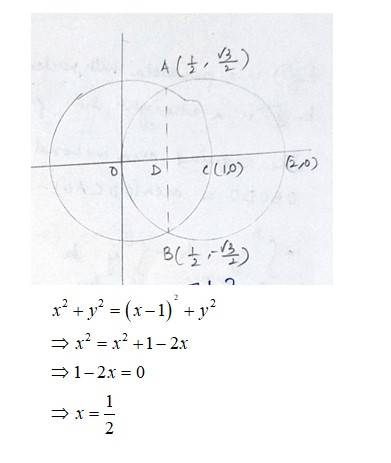

New answer posted
6 months agoContributor-Level 10
The equation given circle is
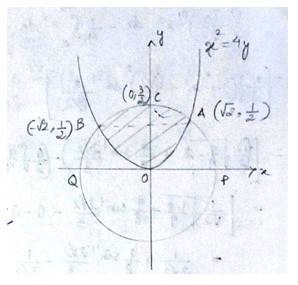
i.e, centre (0,0), radius
since intersect the circle
we can put in
which is not possible or cannot be (-)ve


New answer posted
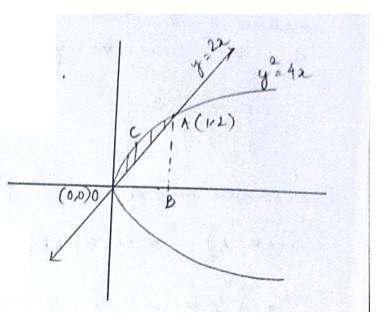
6 months agoContributor-Level 10
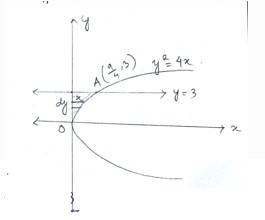
As intersect at Athen,
A has coordinate
Hence, area of curve =
Option (B) is correct
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 679k Reviews
- 1800k Answers