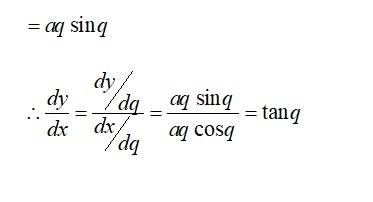Maths

17. We can write the given statement as:-

$\frac{1}{3\cdot 5}+\frac{1}{5\cdot 7}+\frac{1}{7\cdot 9}+?+\frac{1}{(2n+1)(2n+3)}=\frac{n}{3(2n+3)}$

For n = 1,

We get $P(1)=\frac{1}{3\cdot 5}=\frac{1}{15}=\frac{1}{3(2\cdot 1+3)}=\frac{1}{3(2+3)}=\frac{1}{3*5}=\frac{1}{15}$

Which is true.

Consider P(k) be true for some positive integer k.

$P(K)=\frac{1}{3\cdot 5}+\frac{1}{5\cdot 7}+\frac{1}{7\cdot 9}+\dots +\frac{1}{(2k+1)(2k+3)}=\frac{k}{3(2k+3)}$ (1)

Now, let us prove that P(k+ 1) is true.

Now,

P(k +1) = $1$ $\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+...+\frac{1}{(2k+1)(2k+3)}+\frac{1}{[2(k+1)+1][2(k+1)+3]}$

By using (1),

$\begin{array}{l}=\frac{k}{3(2k+3)}+\frac{1}{(2k+2+1)(2k+2+3)}\\ =\frac{k}{3(2k+3)}+\frac{1}{(2k+3)(2k+5)}\\ =\frac{1}{(2k+3)}\left[\frac{k}{3}+\frac{1}{(2k+5)}\right]\\ =\frac{1}{(2k+3)}\left[\frac{k(2k+5)+3}{3(2k+5)}\right]\end{array}$

$=\frac{1}{(2k+3)}\left[\frac{2k^2+5k+3}{3(2k+5)}\right]$

= $\frac{1}{2k+3}\left[\frac{2k^2+2k+3k+3}{3(2k+5)}\right]$

$=\frac{1}{2k+3}\{\frac{2k(k+1)+3(k+1)}{3(2k+1)}\}$

$\begin{array}{l}=\frac{1}{(2k+3)}\frac{(2k+3(k+1)}{\cdot (2k+1)\cdot 3}\\ =\frac{k+1}{3(2k+5)}\\ =\frac{(k+1)}{3\{2(k+1)+3\}}\end{array}$

P(k+ 1) is true wheneverP(k) is true.

Therefore, from the principle of mathematical induction, theP(n) is true for all natural number n.

Given: Equation of the family of curves  $y=e^{2x}\left(a+bx\right)..........(1)$

Differentiating both sides with respect to x, we get:

$\begin{array}{l}{y}^{\text{'}}=2e^{2x}\left(a+bx\right)+e^{2x}.b\\ \Rightarrow y^{\text{'}}=e^{2x}\left(2a+2bx+b\right)..........(2)\end{array}$

Multiplying equation (1) with (2) and then subtracting it from equation (2), we get:

$\begin{array}{l}{y}^{\text{'}}-2y=e^{2x}\left(2a+2bx+b\right)-e^{2x}\left(2a+2bx\right)\\ \Rightarrow y^{\text{'}}-2y=b{e}^{2x}..........(3)\end{array}$

Differentiating both sides with respect to x, we get:

$y^{"}-2y^{\text{'}}=2b{e}^{2x}..........(4)$

Dividing equation (4) by equation (3), we get:

$\begin{array}{l}\frac{y^{"}-2y^{\text{'}}}{y^{\text{'}}-2y}=2\\ \Rightarrow y^{"}-2y^{\text{'}}=2y^{\text{'}}-4y\\ \Rightarrow y^{"}-4y^{\text{'}}+4y=0\end{array}$

This is the required differential equation of the given curve.

16. Let the given statement as

P(n)= $\frac{1}{1.4}+\frac{1}{4.7}+\frac{1}{7.10}$ + … + $\frac{1}{(3n-2)(3n+1)}=\frac{n}{(3n+1)}$

If n=1, then

P(1)= $\frac{1}{1.4}$ = $\frac{1}{4}$ = $\frac{1}{(3.1+1)}$ = $\frac{1}{4}$

which is true.

Consider P(k)be true for some positive integer k

P(k)= $\frac{1}{1.4}+\frac{1}{4.7}+\frac{1}{7.10}$ + … + $\frac{1}{(3k-2)(3k+1)}$ = $\frac{k}{(3k+1)}$ ------------------(1)

Now, let us prove P(k+1) is true.

P(k+1)= $\frac{1}{1.4}+\frac{1}{4.7}+\frac{1}{7.10}$ + … + $\frac{1}{(3k-2)(3k+1)}+\frac{1}{[3(k+1)-2][3(k+1)+1]}$

By using (1),

$\frac{k}{(3k+1)}+\frac{1}{(3k+3-2)(3k+3+1)}$

= $\frac{k}{(3k+1)}+\frac{1}{(3k+1)(3k+4)}$

= $\frac{1}{(3k+1)}\left\{k+\frac{1}{3k+4}\right\}$

= $\frac{1}{(3k+1)}\left\{\frac{k(3k+4)+1}{3k+4}\right\}$

= $\frac{1}{(3k+1)}\left\{\frac{3k^2+4k+1}{3k+4}\right\}$

= $\frac{1}{(3k+1)}\left\{\frac{3k^2+3k+k+1}{3k+4}\right\}$

= $\frac{1}{(3k+1)}\left\{\frac{3k(k+1)+(k+1)}{3k+4}\right\}$

= $\frac{1}{(3k+1)}\frac{(3k+1)(k+1)}{3k+4}$

= $\frac{k+1}{3k+4}=\frac{k+1}{3(k+1)+1}$

? P(k+1) is true whenever P(k) is true.

Therefore, from the principle of mathematical induction, the P(n) is true for all natural number n.

Given: Equation of the family of curves  $y=a{e}^{3x}+b{e}^{-2x}..........(i)$

Differentiating both sides with respect to x, we get:

$y^{\text{'}}=3a{e}^{3x}-2b{e}^{-2x}..........(ii)$

Again, differentiating both sides with respect to x, we get:

$y^{"}=9a{e}^{3x}-4b{e}^{-2x}..........(iii)$

Multiplying equation (i) with (ii) and then adding it to equation (ii), we get:

$\begin{array}{l}\left(2a{e}^{3x}+2b{e}^{-2x}\right)+\left(3a{e}^{3x}-2b{e}^{-2x}\right)=2y+y^{\text{'}}\\ \Rightarrow 5a{e}^{3x}=2y+y^{\text{'}}\\ \Rightarrow a{e}^{3x}=\frac{2y+y^{\text{'}}}{5}\end{array}$

Now, multiplying equation (i) with (iii) and subtracting equation (ii) from it, we get:

$\begin{array}{l}\left(3a{e}^{3x}+2b{e}^{-2x}\right)-\left(3a{e}^{3x}-2b{e}^{-2x}\right)=3y-y^{\text{'}}\\ \Rightarrow 5b{e}^{-2x}=3y-y^{\text{'}}\\ \Rightarrow b{e}^{-2x}=\frac{3y-y^{\text{'}}}{5}\end{array}$

Substituting the values of $a{e}^{3x}$ and $b{e}^{-2x}$ in equation (iii), we get:

$\begin{array}{l}{y}^{"}=9.\frac{\left(2y-y^{\text{'}}\right)}{5}+4\frac{\left(3y-y^{\text{'}}\right)}{5}\\ \Rightarrow y^{"}=\frac{18y+9y^{\text{'}}}{5}+\frac{12y-4y^{\text{'}}}{5}\\ \Rightarrow y^{"}=\frac{30y+5y^{\text{'}}}{5}\\ \Rightarrow y^{"}=6y+y^{\text{'}}\\ \Rightarrow y^{"}-y^{\text{'}}-6y=0\end{array}$

This is the required differential equation of the given curve.

Given: Equation of the family of curves  $y^2=a\left(b^2-x^2\right)$

Differentiating both sides with respect to x, we get:

$\begin{array}{l}2y\frac{dy}{dx}=a\left(-2x\right)\\ \Rightarrow 2y{y}^{\text{'}}=-2ax\\ \Rightarrow y{y}^{\text{'}}=-ax..........(1)\end{array}$

Again, differentiating both sides with respect to x, we get:

$\begin{array}{l}{y}^{\text{'}}.y^{\text{'}}+y{y}^{"}=-a\\ \Rightarrow {\left(y^{\text{'}}\right)}^2+y{y}^{"}=-a..........(2)\end{array}$

Dividing equation (2) by equation (1), we get:

$\begin{array}{l}\frac{{\left(y^{\text{'}}\right)}^2+y{y}^{"}}{y{y}^{\text{'}}}=\frac{-a}{-ax}\\ \Rightarrow xy{y}^{"}+x{\left(y^{\text{'}}\right)}^2-y{y}^{"}=0\end{array}$

This is the required differential equation of the given curve.

94. Kindly go through the solution

Given: Equation of the family of curves  $\frac{x}{a}+\frac{y}{b}=1..........(i)$

Differentiating both sides of the given equation with respect to x, we get:

$\begin{array}{l}\frac{1}{a}+\frac{1}{b}\frac{dy}{dx}=0\\ \Rightarrow \frac{1}{a}+\frac{1}{b}{y}^{\text{'}}=0\end{array}$

Again, differentiating both sides with respect to x, we get:

$\begin{array}{l}0+\frac{1}{b}{y}^{"}=0\\ \Rightarrow \frac{1}{b}{y}^{"}=0\\ \Rightarrow y^{"}=0\end{array}$

Hence, the required differential equation of the given curve is $y^{"}=0$

15. We can write the given statement as

P(n)=1²+3²+5²+ … + (2n – 1)²= $\frac{n(2n-1)(2n+1)}{3}$

forn=1

P(1)=1²=1= $\frac{1(2.1-1)(2.1+1)}{3}$

= $\frac{1(1)(3)}{3}=1$ which is true.

Consider P(k) be true for some positive integer k

P(k)=1²+3²+5²+ … + (2n – 1)²= $\frac{k(2k-1)(2k+1)}{3}$ ------------------(1)

Now, let us prove that P(k+1) is true.

Here,

1²+3²+5²+ … +(2k – 1)²+(2(k+1) –1)²

By using (1),

$\frac{k(2k-1)(2k+1)}{3}+{[2k+2-1)}^2$

= $\frac{k(2k-1)(2k+1)+3{(2k+1)}^2}{3}$

= $\frac{(2k+1)[k(2k-1)+3(2k+1)]}{3}$

= $\frac{(2k+1)\left(2k^2-k+6k+3\right)}{3}$

= $\frac{(2k+1)\left(2k^2+5k+3\right)}{3}$

we can write as,

= $\frac{(2k+1)\left(2k^2+2k+3k+3\right)}{3}$

= $\frac{(2k+1)\{2k(k+1)+3(k+1)\}}{3}$

= $\frac{(2k+1)(2k+3)(k+1)}{3}$

= $\frac{(2k+1)(k+1)(2k+3)}{3}$

= $\frac{(k+1)\{2(k+1)-1\}\{2(k+1)+1\}}{3}$

P(k+1) is true whenever P(k) is true.

Hence, from the principle of mathematical induction, the P(n) is true for all natural number n.

93. Kindly go through the solution

14. Let the given statement be P(n) i.e.,

P(n)= $\left(1+\frac{1}{1}\right)\left(1+\frac{1}{2}\right)\left(1+\frac{1}{3}\right)$ … $\left(1+\frac{1}{n}\right)=(n+1)$

If n =1

P(1)= $\left(1+\frac{1}{1}\right)$ = 2 =1+1= 2

which is true.

Assume that P(k) is true for some positive integer k i.e.,

P(k): $\left(1+\frac{1}{1}\right)\left(1+\frac{1}{2}\right)\left(1+\frac{1}{3}\right)$ … $\left(1+\frac{1}{k}\right)=(k+1)$ .---------------------(1)

Now, let us prove that P(k+1) is true.

Here,

P(k+1)= $\left(1+\frac{1}{1}\right)\left(1+\frac{1}{2}\right)\left(1+\frac{1}{3}\right)$ … $\left(1+\frac{1}{k}\right)+\left(1+\frac{1}{(k+1)}\right)$

By using (1), we get

(k+1). $\left(1+\frac{1}{k+1}\right)$

L.C.M.=(k+1). $\left(\frac{k+1+1}{k+1}\right)$

= (k+1)+1

? P(k+1) is true whenever P(k) is true.

Therefore from the principle of mathematical induction the P(n) is true for all natural numbers n.