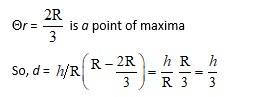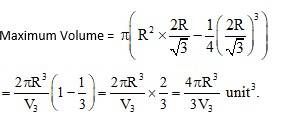Ncert Solutions Maths class 12th

The equation of the given curve is $2y+x^2=3$ .

Differentiate with respect to x, we have:

$\begin{array}{l}\frac{2dy}{dx}+2x=0\\ \Rightarrow \frac{dy}{dx}=-x\\ \therefore {\frac{dy}{dx}]}_{(1,1)}=-1\end{array}$

The slope of the normal to the given curve at point (1,1) is

$\frac{-1}{{\frac{dy}{dx}]}_{(1,1)}}=-1$

Hence, the equation of the normal to the given curve at (1,1) is given as:

$\begin{array}{l}\Rightarrow y-1=1(x-1)\\ \Rightarrow y-1=x-1\\ \Rightarrow x-y=0\end{array}$

Therefore, option (B) is correct.

The equation of the tangent to the given curve is $y=mx+1.$

Now, substituting $y=mx+1.$ in $y^2=4x,$ we get:

$\begin{array}{l}\Rightarrow {\left(mx+1\right)}^2=4x\\ \Rightarrow m^2{x}^2+1+2mx-4x=0\\ \Rightarrow m^2{x}^2+x(2m-4)+1=0..........(i)\end{array}$

Since a tangent touches the curve at one point, the roots of equation (i) must be equal.

Therefore, we have:

Discriminant = 0

$\begin{array}{l}{(2m-4)}^2-4{(m)}^2(1)=0\\ \Rightarrow 4m^2+16-16m-4m^2=0\\ \Rightarrow 16-16m=0\\ \Rightarrow m=1\end{array}$

Hence, the required value of m is 1.

Therefore, option (A) is correct.

Let x be the depth of the wheat inside the cylindrical tank is with radius = 10 cm

Then, Volume V of the cylindrical tank is

V = π (10)²x = 100πpx m³

As $\frac{d}{dt}=314\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$h$}\right.$

$\Rightarrow 100\pi \frac{dx}{dt}=314$

$\frac{dx}{dt}=\frac{314}{100\pi }=\frac{314}{100\pi 3.14}=\frac{314}{314}=1.\raisebox{1ex}{$m$}\!\left/ \!\raisebox{-1ex}{$h$}\right.$ i e, rate of increasing of depth

option (A) is correct

Kindly go through the solution

Kindly go through the solution

We have,

f (x) defined on [a, b]

And f (x) > 0 ∀ x ∈ [a, b].

Let x₁, x₂ ∈ [a, b] and x₂>x₁

In the internal x₁, x₂], f (x) will also be continuous and differentiable.

Hence by mean value theorem, there exist c [x₁, x₂] such that

$f(c)=\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_{1.}}$

f (x) > 0 ∀ x ∈ [a, b].

Then, f (c) > 0.

$\Rightarrow \frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}>0$

i.e., f (x₂) -f (x₁) > 0

f (x₂) >f (x₁).

Hence, the function f (x) is always increasing on [a, b]

Let x be the radius of the sphere ad x be radius of the right circular cone.

Let height of cone = y

Then, in ΔOBA,

(y-r)² + x² = r²

y² + r²- 2ry + x² = r²

x²=2ry - y²

So, the volume V of the cone is

$V=\frac{1}{3}\pi ·x^2·y$ $\left\{=\frac{1}{3}\pi {(radius)}^2*hight\right\}$

$=\frac{1}{3}*\left(2xy-y^2\right)y$

$=\frac{1}{3}x\left(2x{y}^2-y^3\right).$

So, $\frac{dv}{dy}=\frac{\pi }{3}\left[4xy-3y^2\right]$

And $\frac{d^2}{d{y}^2}=\frac{x}{3}[4x-6y].$

At $\frac{dV}{dy}=0.$

$\Rightarrow \frac{\pi }{3}\left[4xy-3y^2\right]=0$

4x -y- 3y² = 0

$\Rightarrow y=\frac{4x}{3}$ asy> 0.

At y = $\frac{4\pi }{3},\frac{d^{2}v}{d{y}^2}=\frac{\pi }{3}[4x-8x]$ = $-\frac{4\pi r}{3}<0.$

Ø V is maximum when y = $\frac{4\pi }{3}$

We have,

f (x) = cos²x + sin x, x∈ [0, π ].

So, f (x) = 2 cos x ( -sin x) + cos x = cos x (1 - 2 sin x).

At f (x) = 0

cosx (1 - 2 sin x) = 0

cosx = 0  or  1 - 2 sin x = 0

cosx = cos $\frac{\pi }{2}$ or sin x = $\frac{1}{2}$ = sin $\frac{\pi }{6}$ = sin $x-\frac{\pi }{6}$

x= $\frac{\pi }{2}$ , x = $\frac{\pi }{6}$ and x = $\frac{5\pi }{6}$  [0, π ].

So, f $\left(\frac{\pi }{2}\right)$ = cos²$\frac{\pi }{2}$ + sin $\frac{\pi }{2}$ = 1.

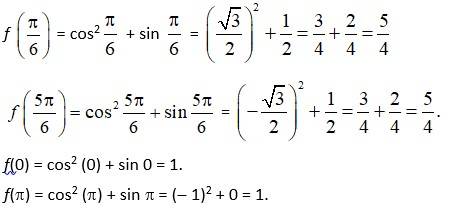
Absolute minimum of f (x) = $\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$ and absolute minimum of f (x) = 1.

Let P be the point on hypotenuse of a triangle. ABC, t angle at B.

Which is at distance a& b from the sides of the triangle.

Let < BAC = < MPC = .

Then, in… ΔANP,

$\Rightarrow ta{n}^3\theta =\frac{a}{b}$

$tan\theta ={\left(\frac{a}{b}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right..}$

At tan Ø = ${\left(\frac{a}{b}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3,$}\right.}$

$\frac{d^2\stackrel{?}{q}}{d{\theta }^2}=+ve.>0.$ { Øall trigonometric fxⁿ are + ve in I^st quadrant}.

So, z is least for tanØ = ${\left(\frac{a}{b}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3.$}\right.}$

As, Sec²Ø = 1 + tan²Ø = 1 + ${\left(\frac{a}{b}\right)}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3.$}\right.}$ = $\frac{b^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}+a^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}{b^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3.$}\right.}}$

secØ = ${\left[\frac{b^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}+a^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}{b^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$ = $\frac{{\left(a^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}+b^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{b^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right..}}$

And tan²Ø = $\frac{1}{co{t}^2\theta }$

cot²Ø = ${\left(\frac{a}{b}\right)}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}$

And cosec²Ø = 1 + cot²Ø = 1 + ${\left(\frac{a}{b}\right)}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}$ = $\frac{a^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}+b^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}{a^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}$

cosecØ = $\frac{{\left(a^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}+b^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right..}}{a^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}$