Ncert Solutions Maths class 12th
Get insights from 2.5k questions on Ncert Solutions Maths class 12th, answered by students, alumni, and experts. You may also ask and answer any question you like about Ncert Solutions Maths class 12th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
4 months agoContributor-Level 10
Let 'x' metre be the radius of the semi-circular opening mounded on the length '2x' side of rectangle. Then, let 'y' be the breadth of the rectangle.
Then, perimeter of the window = 10m
x + 2x + 2y + = 10.
Let the area of the window be A.
Then, A =
= [-πx2- 4x2 + 20x].
So, [ -2πx - 8x + 20]
And [ -2π - 8] = -π -4 = -( π+ 4)
At
[ -2πx - 8x + 20] = 0
2x + 8x = 20
x = =
At x = = -( π+ 4) < 0
Øx = is a point of minima.
And y =
Ø Dimensions of the window are
length = 2x =
breadth = y
radius = y =
New answer posted
4 months agoContributor-Level 10
Let r and s be the radius of the circle and length of side of square.
Then, sum of perimeter of circle and square = k
2πr +4s = k
s =
The area A be the total areas of the circle and square.
Then, A = πr2 + s2
So,
And
At
At
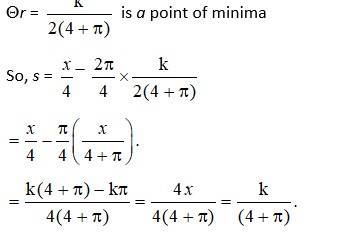
s =
s = 2r.
Hence, proved.
New answer posted
4 months agoContributor-Level 10
Let x and y meters be the length and breath of the rectangular base of the tank respectively.
Then, volume V of the tank is
V = length * depth * breath.
V = 2xy = 8m3(given).
Let 't' be the total cost of building the tank.
Then, t = cost of base + cost of sides.
= 70xy + 45[4x+4y] {there are four sides.
= 70xy + 180x+ 180y.
=
So,
And
At
x = ± 2
x = 2, (x = length and it cannot be negative)
At x = 2,
x = 2 is point of maxima.
Hence, minimum cost = = 280 + 360 + 360 = 1000.
New answer posted
4 months agoContributor-Level 10
The given equation of the ellipse is (1)
Let the major axis be along x-axis so, vertex is at
Let ΔABC be the isosceles triangle inscribed on the
ellipse with one vertex C at (a, 0).
Then, let A have Co-ordinate (x0, yo) from figure.
So, Co-ordinate of B = (x0, y0)
As A and B lies on the ellipse, from equation (i),




New answer posted
4 months agoContributor-Level 10
We have, f(x) =
{
At
So we have three disjoint internal i.e.,
When,
So, f(x) is increasing.
When
So, f(x) is decreasing.
When
f(x) =
So, f(x) is increasing.
f(x) is increasing for x(∞,1) and [1, ∞] and decreasing for x[1, 1].
New answer posted
4 months agoContributor-Level 10
We have, f(x)=
So,
Now,
And, as cos x lies in [1, 1].
So, (i) for increasing, f(x) ≥ 0.
cosx ≥ 0.
x lies in Ist and IVth quadrant.
i.e., f(x) is increasing for and
(ii) for decreasing, f(x) ≤ 0.
cosx ≤ 0.
x lies in IInd and IIIrd quadrant.
i.e., f(x) is decreasing for .
New answer posted
4 months agoContributor-Level 10
We have
Slope of the normal at any point is
The equation of the normal at a given point is given by,
Now, the perpendicular distance of the normal from the origin is
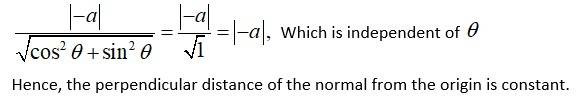
New answer posted
4 months agoContributor-Level 10
Equation of the curve is
Now, the slope of the normal at point is
Equation of the normal at is
New answer posted
4 months agoContributor-Level 10
Let 'b' and 'x' be the fixed base and equal side of isosceales triangle.
Then, cm/s (Ø decreasing).

New answer posted
4 months agoContributor-Level 10
We have, f(x)
f(x) =
f(x) =
=
= =
At extreme points, f(x) = 0.
At x = e, f"(e) =
x = e is a point of maximum.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 687k Reviews
- 1800k Answers
