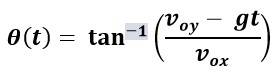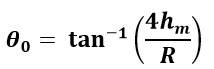ncert solutions physics class 11th

Get insights from 149 questions on ncert solutions physics class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about ncert solutions physics class 11th

149
Questions
0
Discussions
0
Active Users
11
Followers

Have a question about ncert solutions physics class 11th? Ask our experts

Ask Your Question

Keep it short & simple. Type complete word. Avoid abusive language.

New answer posted•a year ago

ncert solutions physics class 11th Motion in a Plane

4.31 A cyclist is riding with a speed of 27 km/h. As he approaches a circular turn on the road of radius 80 m, he applies brakes and reduces his speed at the constant rate of 0.50 m/s every second. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn?

83 Views|Posted a year ago

Asked by Vishal Baghel

Answered by

Vishal Baghel | Contributor-Level 10

a year ago

4.31

Speed of the cyclist = 27 km/h = 7.5 m/s

Radius of the road = 80m

The net acceleration is due to braking and the centripetal acceleration

Acceleration due to braking = 0.5 m/s²

Centripetal acceleration a = v²r = (7.5)2/80= 0.703 m/s²

The resultant acceleration is given by a = sqrt ( $a_{t}^{2}$ +

Upvote

New answer posted•a year ago

ncert solutions physics class 11th Motion in a Plane

4.30 A fighter plane flying horizontally at an altitude of 1.5 km with speed 720 km/h passes directly overhead an anti-aircraft gun. At what angle from the vertical should the gun be fired for the shell with muzzle speed 600 m s^-1 to hit the plane ? At what minimum altitude should the pilot fly the plane to avoid being hit ? (Take g = 10 m s^-2 ).

153 Views|Posted a year ago

Asked by Vishal Baghel

Answered by

Vishal Baghel | Contributor-Level 10

a year ago

4.30

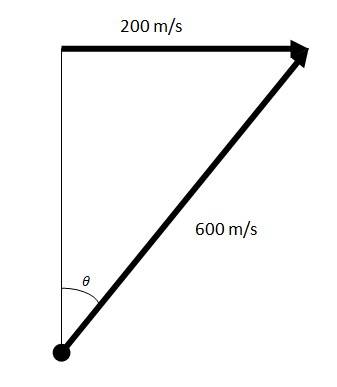
Speed of the fighter plane = 720 km/h = 200 m/s

The altitude of the plane = 1.5 km =1500 m

Velocity of the shell = 600 m/s

$\sin ? θ$ = 200/600

$∴ θ = 19.47 °$

Let H be the minimum altitude for the plane to fly, without being hit

Using equation H = $u^{2}$ sin2 (90- $θ) / 2 g$

= (6002cos2 $θ$ )/2g

= 360000 { ( 1 + co

Upvote

New answer posted•a year ago

ncert solutions physics class 11th Motion in a Plane

4.29 A bullet fired at an angle of 30° with the horizontal hits the ground 3.0 km away. By adjusting its angle of projection, can one hope to hit a target 5.0 km away? Assume the muzzle speed to be fixed, and neglect air resistance.

269 Views|Posted a year ago

Asked by Vishal Baghel

Answered by

Vishal Baghel | Contributor-Level 10

a year ago

4.29 The angle of projectile $θ$ = 30 $°$

The bullet hits the ground at a distance of 3 km, Range R = 3 km

We know horizontal range for a projectile motion, R = $u^{2}$ sin2 $θ$ / g

3 = $u^{2}$ sin60 $°$ / g

$\frac{u^{2}}{g}$ = 3/ sin60 $°$ = 3.464 …………… (1)

To hit a target at 5 k

Upvote

New answer posted•a year ago

ncert solutions physics class 11th Motion in a Plane

4.28 Can you associate vectors with

(a) The length of a wire bent into a loop

(b) A plane area

(c) A sphere?

Explain.

7 Views|Posted a year ago

Asked by Vishal Baghel

Answered by

Vishal Baghel | Contributor-Level 10

a year ago

4.28

(a) We cannot associate the length of a wire bent into a loop with a vector.

(b) We can associate a plane area with a vector.

(c) We cannot associate the volume of a sphere with a vector.

Upvote

New answer posted•a year ago

ncert solutions physics class 11th Motion in a Plane

4.27 A vector has both magnitude and direction. Does it mean that anything that has magnitude and direction is necessarily a vector? The rotation of a body can be specified by the direction of the axis of rotation, and the angle of rotation about the axis. Does that make any rotation a vector?

13 Views|Posted a year ago

Asked by Vishal Baghel

Answered by

Vishal Baghel | Contributor-Level 10

a year ago

4.27 No in the both the cases.

A physical quantity which is having both direction and magnitude is not necessarily a vector. For instance, in spite of having direction and magnitude, current is a scalar quantity. The basic necessity for a physical quantity to fall in a vector category is that it ough

Upvote

New answer posted•a year ago

ncert solutions physics class 11th Motion in a Plane

4.26 A vector has magnitude and direction. Does it have a location in space? Can it vary with time? Will two equal vectors a and b at different locations in space necessarily have identical physical effects? Give examples in support of your answer.

32 Views|Posted a year ago

Asked by Vishal Baghel

Answered by

Vishal Baghel | Contributor-Level 10

a year ago

4.26 Yes and No

A vector in space has no distinct location. The reason behind this is that a vector stays unchanged when it displaces in a way that its direction and magnitude do not change.

A vector changes with time. For instance, the velocity vector of a ball moving with a specific speed fluctuates

Upvote

New question posted•a year ago

ncert solutions physics class 11th Classification of Elements and Periodicity in Prop

<p>MMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMM</p>

4 Views|Posted a year ago

Asked by Akanksha

New answer posted•a year ago

ncert solutions physics class 11th Physics Gravitation

8.25 A rocket is fired ‘vertically’ from the surface of mars with a speed of 2 km s–1. If 20% of its initial energy is lost due to Martian atmospheric resistance, how far will the rocket go from the surface of mars before returning to it? Mass of mars = 6.4×10²³ kg; radius of mars = 3395 km; G = 6.67×10^-11 N m² kg^–2.

8 Views|Posted a year ago

Asked by Vishal Baghel

Answered by

Vishal Baghel | Contributor-Level 10

a year ago

Initial kinetic energy of the rocket = $\frac{1}{2} {m v}^{2}$

Initial potential energy of the rocket = $\frac{- G M m}{R}$

Total initial energy = $\frac{1}{2} {m v}^{2} - \frac{G M m}{R}$

If 20% of initial kinetic energy is lost due to Martian atmosphere resistance, then only 80% of its kinetic energy helps in reaching a height

Total initial energy available = 0.8

Upvote

New answer posted•a year ago

ncert solutions physics class 11th Physics Gravitation

8.24 A spaceship is stationed on Mars. How much energy must be expended on the spaceship to launch it out of the solar system? Mass of the space ship = 1000 kg; mass of the sun = 2×10³⁰ kg; mass of mars = 6.4×10²³ kg; radius of mars = 3395 km; radius of the orbit of mars = 2.28 ×10⁸ km; G = 6.67×10^-11 N m2 kg^–2.

4 Views|Posted a year ago

Asked by Vishal Baghel

Answered by

Vishal Baghel | Contributor-Level 10

a year ago

Mass of the spaceship, $m_{s}$ = 1000 kg

Mass of the Sun, M = 2 × 10³⁰ kg

Mass of Mars, $m_{m}$ = 6.4×10²³ kg

Orbital radius of Mars, R = 2.28 ×10⁸ km = 2.28 ×10¹¹ m

Radius of Mars, r = 3395 km = 3.395 $\times 10^{6} m$

Universal Gravitational constant, G = 6.67×10^-11 N m2 kg–2

Potential energy of the spaceship due

Upvote

New answer posted•a year ago

ncert solutions physics class 11th Physics Gravitation

8.23 A star 2.5 times the mass of the sun and collapsed to a size of 12 km rotates with a speed of 1.2 rev. per second. (Extremely compact stars of this kind are known as neutron stars. Certain stellar objects called pulsars belong to this category). Will an object placed on its equator remain stuck to its surface due to gravity? (mass of the sun = 2×10³⁰ kg).

8 Views|Posted a year ago

Asked by Vishal Baghel

Answered by

Vishal Baghel | Contributor-Level 10

a year ago

Yes, a body gets stuck to the surface of a star if the inward gravitational force is greater than the outward centrifugal force caused by the rotation of the star.

Gravitational force, $f_{g}$ = $\frac{G M m}{R^{2}}$ , where M = mass of the star = 2.5 $\times 2 \times 10^{30}$ = 5 $\times 10^{30}$ kg

M = mass of the body, R = rad

Upvote

ncert solutions physics class 11th

Questions

Discussions

Active Users

Followers