Gravitation: Class 11 Physics Notes, Meaning, Kepler's Laws, Gravitational Strength, and More

Gravitation is the force of attraction between any two objects with mass. This force depends on the mass of and the distance between the objects. 

Gravity or gravitation is conditional in two ways. 

1. The more the mass of the objects, the stronger the pull. 
2. The closer the distance between the objects, the stronger the pull. 

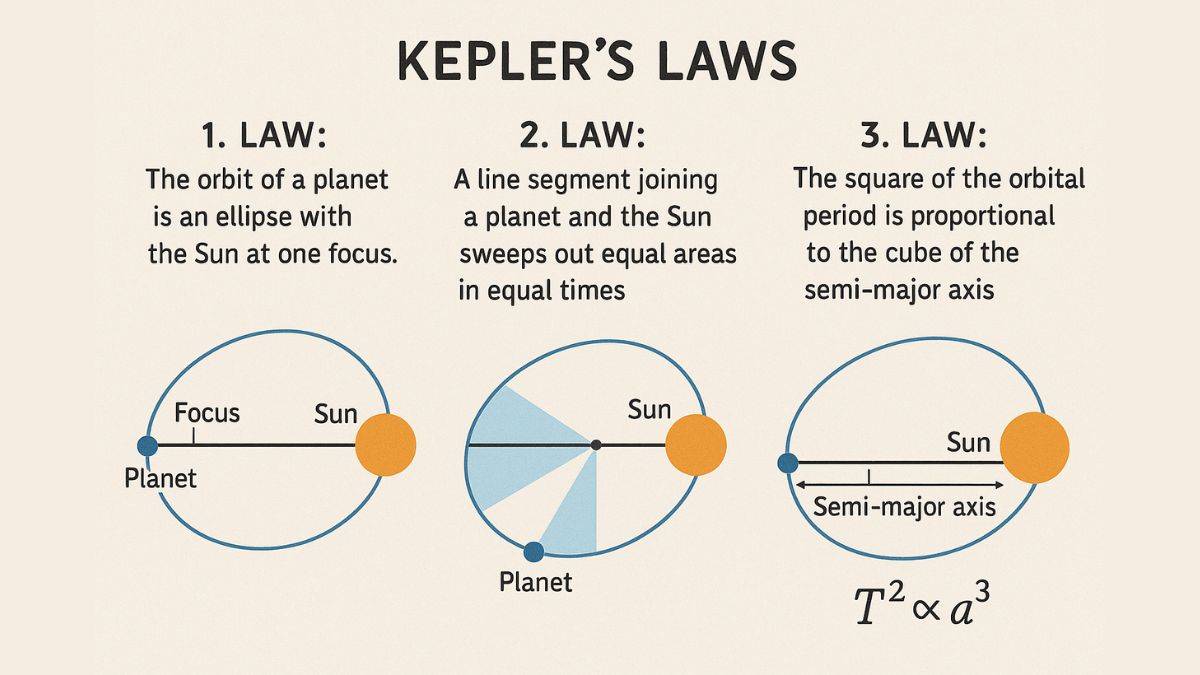
This meaning of gravitation is what Newton deciphered as the Universal Law of Gravitation.  He used his mathematical calculated based on Kepler’s celestial/planetary motion and Galileo’s terrestrial motion.  That’s why it is essential to have a glimpse of Kepler’s Laws.

Johannes Kepler is known for Kepler’s Laws that define the movement of planets around the Sun. These laws were based on the fairly new Copernican model at that time that showed that planets have orbits and move around the Sun, and not the other way around as Ptolemy put it with the geocentric view. 

Quick Note: Heliocentric view is about the Sun being at the centre of the solar system, where planets revolve around it. While the Geocentric view was the Earth being the centre of the solar system while celestial bodies or planets revolved around it. 

Let’s view the three of Kepler’s Laws. 

1. Law of Orbits
2. Law of Areas
3. Law of Periods

Kepler’s Law of Orbits states that all planets move around the sun. Each of the planets has an elliptical orbit, with the Sun at one focus. 

The Law of Areas of Kepler is the second law that states the planets closer to the sun move faster in the orbit and when away, they move slower. Both these movements cover equal areas and equal time in the orbit. The reason for this is that the angular momentum stays constant. 

Note: Angular momentum is how much an object spins or orbits. For forces like gravity that pulls towards a centre, the spinning or orbiting tendency remains the same. 

The third law of Kepler is the Law of Periods. It states that the square of the planet’s orbital period is directly proportional to the cube of the semi-major axis of the orbit. 

Mathematically, we represent that as 

  T² ∝ a³

T² as the square of the planet’s orbital period

a³ as the cube of the semi-major axis

What’s Orbital Period? Orbital period is the total time taken to complete one full circle around the Sun. For instance, the Earth’s orbital period is one year. 

What’s Semi-Major Axis? It’s the longest radius of the elliptical orbit, or the average distance of the planet from the sun.

 

 

 

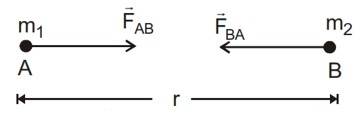
All physical bodies are subject to the action of the forces of mutual gravitational attraction, which is Newton's Law of Universal Gravitation.
The law is stated as: "Between any two particles of masses $m_1$ and $m_2$ at separation $r$ from each other there exist attractive forces ${\vec{F}}_{AB}$ and ${\vec{F}}_{BA}$ directed from one body to the other and equal in magnitude which is directly proportional to the product of the masses of the bodies and inversely proportional to the square of the distance between the two".

So, we can write

$F_{AB}=F_{BA}=G\frac{m_1{m}_2}{r^2}$

Where G is the Universal Gravitational Constant.

This value is equal to $6.67\times {10}^{-11}{\mathrm{N}\mathrm{m}}^2/\mathrm{k}\mathrm{g}$

The law of gravitation can be applied to bodies whose dimensions are small compared to the separation between or when bodies can be treated as point particles.

If the bodies are not very small, we can not directly apply the expression in equation (1) to find their natural gravitational attraction. In this case, we use the following procedure to see the same. The bodies are initially split into small parts or many point masses. Using equation (1), the force of attraction exerted on a particle of one body by a particle of another body can be obtained. Now we add all forces vectorially exerted by all independent particles of the second body on the particle of the first body. Finally, the resultants of these forces are summed over all particles of the first body to obtain the net force experienced by the bodies.

In general, we use integration or basic summation of these forces.

• It's a conservative force
• It's a central force
• It is equal in magnitude & opposite in direction
• These forces are an action-reaction pair
• It acts along the line joining the two masses.
• It doesn't depend on the medium
• It's an attractive force.

$\vec{F}=\frac{-G{m}_1{m}_2\vec{r}}{|\vec{r}{|}^3}$

[The head of $\vec{r}$ is placed at that position where we have to evaluate the force]

A gravitational field is any region around a mass where another mass experiences a gravitational force.

According to Newton's Law of Gravitation, every mass creates a gravitational field around it. When another mass is placed within it, it experiences a force. This field is detectable by the force that the first mass applies to the second. 

To understand the gravitational field strength of one mass exerting on or exerted by another, we need to learn about two concepts - 

• Source Mass - It's the object that creates the gravitational field. This is the larger body, like a planet.
• Test Mass -  This object is a small mass introduced into the gravitational field of the source mass. It cannot exert any gravity on the source mass. 

To measure the gravitational field strength, we can look at it in this way, mathematically, 

For any point in space, let's say the test mass is $m_0$

This test mass experiences a force, and we denote that as $\vec{F}$

Now, at that point in space, the gravitational field strength, often denoted by $\vec{g}$ , is $\vec{g}=\frac{\vec{F}}{m_0}$
Gravitational field strength $\vec{g}$ is a vector quantity, i.e., it has both magnitude and direction. 

 

We can also say that the gravitational field strength has the same direction as the force on the test mass. It's just the acceleration a mass would experience at that point in space. 

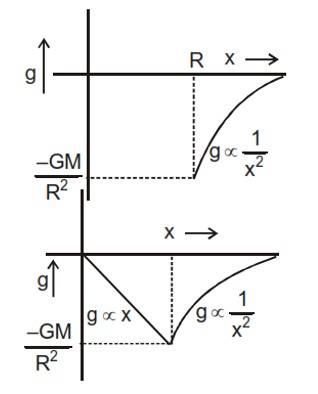
Based on the above, a point mass is an object treated as the mass concentrated at a single point in space. The size of this point mass is considered insignificant. All we should know is that every point mass creates a gravitational field in its surroundings. 

To calculate the gravitational field strength a point mass creates, we place a test mass $m_0$ at a point $P$ . This is at a distance $x$ from a point mass $m$ . The force on $m_0$ is as

$F_g=\frac{Gm{m}_0}{x^2}$

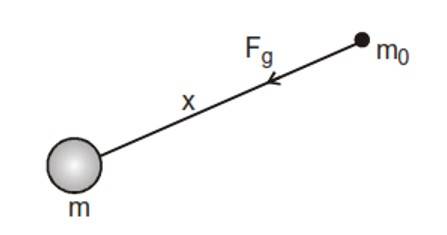
If at point $P$ , the gravitational field strength due to $m$ is  $g_p$

it is 

$g_p=\frac{F_g}{m_0}=\frac{Gm}{x^2}$

The expression here gives the gravitational field strength at a point due to a point mass.

However, this expression is only applicable to the strength of the gravitational field due to point masses. Note that it shouldn't be used for extended bodies.

However, the expression for the gravitational field strength produced by extended masses has already been derived in the electrostatics section, where we replace k by $-\mathrm{G}\&\mathrm{Q}$ by M in that expression.

So we will just revise the expression of gravitational field strength at points due to various extended masses. Gravitational field strength :

1. At a point on the axis of Ring $=\frac{-GMx}{{\left(x^2+R^2\right)}^{3/2}}$

2. At a point on the axis of disc $=\frac{2GM}{R^2}\left[1-\frac{x}{\sqrt[]{R^2+x^2}}\right]$

3. At an axial point of a rod $=\frac{-GM}{L}\left[\frac{1}{x}-\frac{1}{x+L}\right]$

4. Due to a circular $\mathrm{A}\mathrm{r}\mathrm{c}=\frac{-2\mathrm{G}\mathrm{M}\mathrm{s}\mathrm{i}\mathrm{n}(\varphi /2)}{\varphi {\mathrm{R}}^2}$

5. Due to a long, infinite thread $=\frac{-2\mathrm{G}\lambda }{\mathrm{x}}$

6. Due to the long solid cylinder
(a) at an outer point $=\frac{-2\mathrm{G}\rho \pi {\mathrm{R}}^2}{\mathrm{x}}$ (where $\rho$ is mass density per volume)

(b) at an inner point $=-2\mathrm{G}\rho \pi \mathrm{x}$

Due to the hollow sphere
(a) For outer points $=\frac{-GM}{x^2}$ (Behaving as a point mass)
(b) For points on the surface $=\frac{-\mathrm{G}\mathrm{M}}{{\mathrm{R}}^2}$ (Behaving as a point mass)
(c) For inner points $=0$ (As no mass is enclosed within it)

Due to a solid sphere
(a) For outer points $=\frac{-GM}{x^2}$ (Behaving as a point mass)
(b) For points on the surface $=\frac{-GM}{R^2}$ (Behaving as a point mass)
(c) For inner points $=\frac{-\mathrm{G}\mathrm{M}\mathrm{x}}{{\mathrm{R}}^3}$