physics ncert solutions class 11th
Get insights from 951 questions on physics ncert solutions class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about physics ncert solutions class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
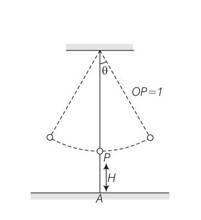
Let us assume t=0 when o then = 0coswt
Given a seconds pendulum w=2
=
At time t, let
Cos2 , t1=1/6
=-( )sin2
t=t1=1/6
d =- sin
the linear velocity is u=-
the vertical component is Uy=
the horizontal component Ux=-
at the time it snaps the vertical height is
H'=H+l(1-cos )
Let the time require for fall be t , then
H'= H+l (1 )
Let the time required for fall be at t then
H'=uyt+1/2 gt2
1/2gt2+
t=
given that is small , hence neglecting terms of order and higher
t=
H'
t=
the distance travelled in the x direction is uxt to the left of where
New answer posted
7 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
The gravitational force on the particle at a distance r from the centre of the earth arises entirely from that portion of matter of the earth in shells internal to the positiin of the particles . the external shells exert no force on the particle.
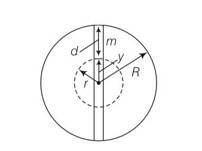
Let g' be the acceleration at P
So g' =g (1-d/R)=g (R-d/R)
R-d=y
g'=gy/R'
F=-mg'= -mgy/R
F
Ma=-Mgy/R, a = -gy/R
Comparing a=-w2y
w2=g/R
T=2
New answer posted
7 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
Let us consider an infinitesimal liquid column of length dx at a height x from horizontal line.
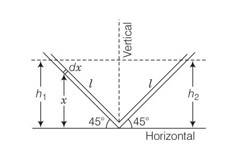
If density of the liquid
PE= dmgx=A
So total PE of the column
= =
But h1=lsin45
PE=A gl2sin245/2
Similarly PE of right column = A gl2sin245/2
Total PE = A gl2sin245/2+ A gl2sin245/2
= A gl2/2
If due to pressure difference is created y element of left side moves on the right side then liquid present in the left arm =l-y
But liquid present in the right arm =l+y
Total PE = PEfinal-PEinitial
Change in PE = ]
= =A
Change in KE = ½ mv2
m=A
change in KE= 1/2A =A
so from
New answer posted
7 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
Let the log be passed and the vertical displacement at the vertical displacement at the equilibrium position
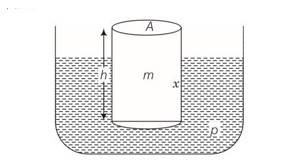
So mg= buoyant forces =
When it is displaced by further displacement x, the buoyant force is A (xo+x)
Net restoring force = buoyant forces -weight
=A (xo+x) -mg
=A
As displacement x is downward and restoring force is upward
Frestoring =-A =-kx
So motion is SHM
Acceleration a=Frestoring/m=-kx/m
a=-w2x
w2=k/m
w=
T= 2
New answer posted
7 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
(a) When the support of the hand is removed the body oscillates about mean position
Suppose x is the maximum extension in the spring when it reaches the lowest point in oscillation.
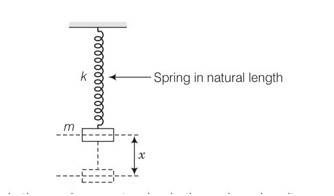
Loss in PE of the block=mgx
Gain in elastic potential energy =1/2 kx2
By energy conservation we cam say that
Mgx=1/2kx2
Or x= 2mg/k
Now the mean position of oscillation will be when the block is balanced by spring
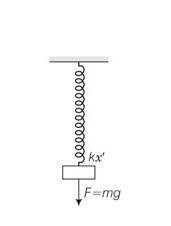
If x' is the extension in that case
F= kx'
F=mg
Mg=kx'
X'=mg/k
By dividing x by x'
x/x'=
so x=2x'
x'=4/2 =2cm
but the displacement of mass from the mean position when spring attains its natural l
New question posted
7 months agoNew answer posted
7 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
(a) The weight of the body changes during oscillations.
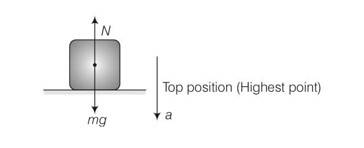
(b) Considering the situations in two extreme positions
we can say mg-N= ma
so at the highest point the platform is accelerating downward.
N=mg-ma
a=w2A
N=mg-mw2A
A= amplitude of motion m=50kg v=2m/s
w=2
A= 5cm = 5
N= 50
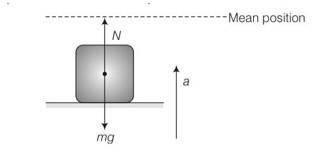
When it is accelerating towards mean position that is vertically upwards
N-mg=ma=Mw2A
N=mg+mw2A
N=m (g+w2A)
N= 50 [9.8+ ]
N= 884N
Machine reads the normal reaction
Maximum weight =884N
Minimum weight=95.5N
New answer posted
7 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
Let us assume t=0 when o then = 0coswt
Given a seconds pendulum w=2
=
At time t, let
Cos2 , t1=1/6
=-( )sin2
t=t1=1/6
d =- sin
the linear velocity is u=-
the vertical component is Uy=
the horizontal component Ux=-
at the time it snaps the vertical height is
H'=H+l(1-cos )
Let the time require for fall be t , then
H'= H+l (1 )
Let the time required for fall be at t then
H'=uyt+1/2 gt2
1/2gt2+
t=
given that is small , hence neglecting terms of order and higher
t=
H'
t=
the distance travelled in the x direction is uxt to the left of where
New answer posted
7 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
The gravitational force on the particle at a distance r from the centre of the earth arises entirely from that portion of matter of the earth in shells internal to the positiin of the particles . the external shells exert no force on the particle.

Let g' be the acceleration at P
So g' =g (1-d/R)=g (R-d/R)
R-d=y
g'=gy/R'
F=-mg'= -mgy/R
F
Ma=-Mgy/R, a = -gy/R
Comparing a=-w2y
w2=g/R
T=2
New answer posted
7 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
Let us consider an infinitesimal liquid column of length dx at a height x from horizontal line.

If density of the liquid
PE= dmgx=A
So total PE of the column
= =
But h1=lsin45
PE=A gl2sin245/2
Similarly PE of right column = A gl2sin245/2
Total PE = A gl2sin245/2+ A gl2sin245/2
= A gl2/2
If due to pressure difference is created y element of left side moves on the right side then liquid present in the left arm =l-y
But liquid present in the right arm =l+y
Total PE = PEfinal-PEinitial
Change in PE = ]
= =A
Change in KE = ½ mv2
m=A
change in KE= 1/2A =A
so from
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 686k Reviews
- 1800k Answers