physics ncert solutions class 11th
Get insights from 952 questions on physics ncert solutions class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about physics ncert solutions class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New question posted
4 months agoNew answer posted
4 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
(i) dimension of h = [ML2T-1]
And c= [LT-1] and dimension of G= [M-1L3T-2]
Let m= kcxhyGz
[ML0T0]= [LT-1]x [ML2T-1]y [M-1L3T-2]z
= [My-zLx+2y+3zT-x-y-2z]
y-z=1
x+2y+3z=0
-x-y-2z=0
On solving these equation we got x= ½ y= ½ and z= -½
So formula will coming out from this is m=k
(ii) L=kcxhyGz
ao [M0LT0]= [LT-1]x [ML2T-1]y [M-1L3T-2]z
= [My-zLx+2y+3zT-x-y-2z]
y-z=0
x+2y+3z=1
-x-y-2z=0
After solving we get x= -3/2 y=1/2 and z=1/2
We got the formula is L=k
(iii)T= kcxhyGz
[M0L0T]= [LT-1]x [ML2T-1]y [M-1L3T-2]z
= [My-zLx+2y+3zT-x-y-2z]
On comparing powers we got x= -5/2 y=1/2 an
New answer posted
4 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
Dimensions of energy is E= [ML2T-2]
Mass m= [M]
Dimension of E= [ML2T-2]
Dimensions of L= [ML-2T-1]
Dimensions of G= [M-1L3T-2]
By using these values [P]= [ML2T-2] 2 -2
= [M1+2-5+2L2+4-6T-2-2+4]
= [M0L0T0]
After we know that P is dimensionless quantity
New answer posted
4 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
As we know that X= a2 b3 c5/2 d-2
Maximum percentage error in X is
=
Mean absolute error in X= rounding off to significant value.
And calculated value would be 2.8 rounding off upto two digits.
New answer posted
4 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
Rate of flow is equal to V=
Dimensions of V or LHS= volume/time=L3/T= [L3T-1]
Dimensions of P= [ML-1T-2]
Dimensions of = [ML-1T-1]
Dimensions of L= [L]
Dimensions of r= [L]
Dimensions of RHS=
So they are in equal in dimensions.
So equation is correct dimensionally.
New answer posted
4 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
Energy E= [ML2T-2]
Let M1, L1 and T1 and M2, L2 and T2 are fundamental quantities for two units
M1=1kg and L1=1m and T1=1s
M2= α kg, L2= β m and T2= γ s
And n1u1=n2u2
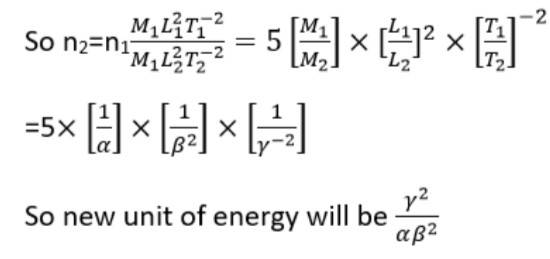
New answer posted
4 months agoContributor-Level 10
This is a multiple choice answer as classified in NCERT Exemplar
Time period of simple pendulum T=2s
For simple pendulum T= where l is length and g = acceleration due to gravity.
Te=2
On the surface of the moon Tm= 2
=
Te=Tm to maintain the second's pendulum time period
1= …………….1
But the acceleration due to gravity at moon is 1/6 of the acceleration due to gravity at earth,
gm=
squaring equation 1 and putting this value
1=
lm=1/6le = 1/6 m
New answer posted
4 months agoContributor-Level 10
This is a multiple choice answer as classified in NCERT Exemplar
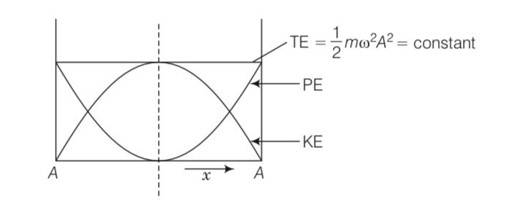
Potential energy of a simple harmonic oscillator is = ½ kx2=1/2mw2x2
K=mw2
When x=0 PE=0
When x= , PE=maximum
=1/2 mw2A2
KE of a simple harmonic oscillator =1/2 mv2
= 1/2 m [w ] 2
= ½ mw2 (A2-x2)
This is also parabola if plot KE against displacement x
KE= 0 at x=
KE=1/2mw2A2 at x=0
Now total energy of the simple harmonic oscillator =PE+KE
= ½ mw2x2+1/2mw2 (A2-x2)
TE= ½ mw2A2
So the curve according to that is
New answer posted
4 months agoContributor-Level 10
This is a multiple choice answer as classified in NCERT Exemplar
As we know x= acoswt
V =dx/dt= a (-sinwt)w=-wasinwt
V=-wasinwt
= wacos ( )
Phase of velocity =
So difference in phse of velocity to that of phase of displacement = =
New answer posted
4 months agoContributor-Level 10
This is a multiple choice answer as classified in NCERT Exemplar
As the particle on reference circle moves in anticlockwise direction. The projection will move from P to O towards left.
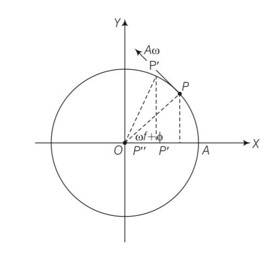
Hence in the position shown the velocity is directed from P' to P'' i.e from right to left . hence sign is negative.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 686k Reviews
- 1800k Answers