Probability

70. Let X represent the number of bulbs that will fuse after 150 days of use in an experiment of 5 trials. The trials are Bernoulli trials.

It is given that, p = 0.05

$\therefore q=1-p=1-0.05=0.95$

X has a binomial distribution with n=5 and $p=0.05$

$={\mathrm{5C}}_x$
$\mathrm{}{\left(0.95\right)}^{5-x}.{\left(0.05\right)}^x$

$P\left(none\right)=P\left(X=0\right)$

$={\mathrm{5C}}_0$
$\begin{array}{l}\mathrm{}{\left(0.95\right)}^5.{\left(0.05\right)}^0\\ =1*{\left(0.95\right)}^5\\ ={\left(0.95\right)}^5\end{array}$

(ii) P (not more than one) $=P\left(X\le 1\right)$

$=P\left(X=0\right)+P\left(X=1\right)\\ =5C_0$
$\mathrm{}{\left(0.95\right)}^5*{\left(0.05\right)}^0+{\mathrm{5C}}_1$
$\begin{array}{l}\mathrm{}{\left(0.95\right)}^4*{\left(0.05\right)}^1\\ =1*{\left(0.95\right)}^5+5*{\left(0.95\right)}^4*{\left(0.05\right)}^1\\ ={\left(0.95\right)}^5+\left(0.05\right){\left(0.95\right)}^4\\ ={\left(0.95\right)}^4*1.2\end{array}$

(iii) P (more than 1) $=P\left(X>1\right)$

$=1-P\left(X\le 1\right)$

$=1-P$ (not more than 1)

$=1-{\left(0.95\right)}^4*1.2$

(iv) P (at least one) $=P\left(X\ge 1\right)$

$=1-p\left(X<1\right)\\ =1-p\left(X=0\right)\\ =1-{\mathrm{5C}}_0$
$\begin{array}{l}\mathrm{}{\left(0.95\right)}^5*{\left(0.05\right)}^0\\ =1-1*{\left(0.95\right)}^5\\ =1-{\left(0.95\right)}^5\end{array}$

69. Let X represent the number of spade cards among the five cards drawn. Since the drawing of card is with replacement, the trials are Bernoulli trials.

In a well shuffled deck of 52 cards, there are 13 spade cards.

$\begin{array}{l}\Rightarrow p=\frac{13}{52}=\frac{1}{4}\\ \therefore q=1-\frac{1}{4}=\frac{3}{4}\end{array}$

X has a binomial distribution with n=5 and $p=\frac{1}{4}$

$={\mathrm{5C}}_x$
$\mathrm{}{\left(\frac{3}{4}\right)}^{5-x}{\left(\frac{1}{4}\right)}^x$

P (all five cards are spades) $=P\left(X=5\right)$

$={\mathrm{5C}}_5$
$\begin{array}{l}\mathrm{}{\left(\frac{3}{4}\right)}^0.{\left(\frac{1}{4}\right)}^5\\ =1.\frac{1}{1024}\\ =\frac{1}{1024}\end{array}$

(ii) P (only 3 cards are spades) $=P\left(X=3\right)$

$=5C_3$
$\begin{array}{l}\mathrm{}{\left(\frac{3}{4}\right)}^2.{\left(\frac{1}{4}\right)}^3\\ =10.\frac{9}{16}.\frac{1}{64}\\ =\frac{45}{512}\end{array}$

(ii) P (none is a spades) $=P\left(X=0\right)$

$={\mathrm{5C}}_0$
$\begin{array}{l}\mathrm{}{\left(\frac{3}{4}\right)}^5.{\left(\frac{1}{4}\right)}^0\\ =1.\frac{243}{1024}\\ =\frac{243}{1024}\end{array}$

68. Let X denote the number of defective items in a sample of 10 items drawn successively. Since the drawing is done with replacement, the trials are Bernoulli trials.

$\begin{array}{l}\Rightarrow p=\frac{5}{100}=\frac{1}{20}\\ \therefore q=1-\frac{1}{20}=\frac{19}{20}\end{array}$

X has a binomial distribution with n=10 and $p=\frac{1}{20}$

$={\mathrm{10C}}_x$

$\mathrm{}{\left(\frac{19}{20}\right)}^{10-x}.{\left(\frac{1}{20}\right)}^x$

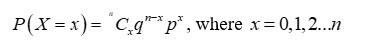
P (not more than 1 defective item) $=P\left(X\le 1\right)$

$=P\left(X=0\right)+P\left(X=1\right)\\ ={\mathrm{10C}}_0$

$\mathrm{}{\left(\frac{19}{20}\right)}^{10}+{\left(\frac{1}{20}\right)}^0+10C_1$
$\begin{array}{l}\mathrm{}{\left(\frac{19}{20}\right)}^9+{\left(\frac{1}{20}\right)}^1\\ ={\left(\frac{19}{20}\right)}^{10}+10{\left(\frac{19}{20}\right)}^9.\left(\frac{1}{20}\right)\\ ={\left(\frac{19}{20}\right)}^9.\left[\frac{19}{20}+\frac{10}{20}\right]\\ ={\left(\frac{19}{20}\right)}^9.\left(\frac{29}{20}\right)\\ =\left(\frac{29}{20}\right).{\left(\frac{19}{20}\right)}^9\end{array}$

67. The repeated tosses of a pair of dice are Bernoulli trials. Let X denote the number of times of getting doublets in an experiment of throwing two dice simultaneously four times.

Probability of getting doublets in a single throw of the pair of dice is

$\begin{array}{l}p=\frac{6}{36}=\frac{1}{6}\\ \therefore q=1-p=1-\frac{1}{6}=\frac{5}{6}\end{array}$

Clearly, X has the binomial distribution with n=4, $p=\frac{1}{6}$ , and $q=\frac{5}{6}$

$\therefore P\left(X=x\right){=}^n{C}_x{q}^{n-x}{p}^x$ , where $x=0,1,2,3...n$

$=4C_x$
$\mathrm{}{\left(\frac{5}{6}\right)}^{4-x}.{\left(\frac{1}{6}\right)}^x\\ =4C_x$
$\begin{array}{l}\mathrm{}.{\frac{5}{6^4}}^{4-x}\end{array}$

$\therefore P$ (2 successes) $=P\left(X=2\right)$

$={\mathrm{4C}}_2$
$\begin{array}{l}\mathrm{}.{\frac{5}{6^4}}^{4-2}\\ =6.\frac{25}{1296}\\ =\frac{25}{216}\end{array}$

66. The repeated tosses of a die are Bernoulli trials. Let X denote the number of successes of getting odd numbers in an experiment of 6 trials.

Probability of getting an odd number in a single throw of a die is, p - 3/6 = 1/2

q = 1 - p = 1/2

X has a binomial distribution.

P (at most 5 successes) $=P\left(X\le 5\right)$

$=1-P\left(X>5\right)\\ =1-P\left(X=6\right)\\ =1-{\mathrm{6C}}_6$
$\begin{array}{l}\mathrm{}{\left(\frac{1}{2}\right)}^6\\ =1-\frac{1}{64}\\ =\frac{63}{64}\end{array}$

66. Let X denote the number of aces obtained. Therefore, X can take any of the values of 0, 1, or 2.

In a deck of 52 cards, 4 cards are aces. Therefore, there are 48 non-ace cards.

X	0	1	2
P (X)	1128/1326	192/1326	6/1326

$Then,E\left(X\right)={\displaystyle \sum _{}^{}{P}_i}{X}_i$

$\begin{array}{l}=0*\frac{1128}{1326}+1*\frac{192}{1326}+2*\frac{6}{1326}\\ =\frac{204}{1326}\\ =\frac{2}{13}\end{array}$

Therefore, option D is correct

65. Let X be the random variable representing a number on the die.

The total number of observations is six.

$\begin{array}{l}\therefore P\left(X=1\right)=\frac{3}{6}=\frac{1}{2}\\ P\left(X=2\right)=\frac{2}{6}=\frac{1}{3}\\ P\left(X=5\right)=\frac{1}{6}\end{array}$

Therefore, the probability distribution is as follows.

$Mean=E\left(X\right)={\displaystyle \sum _{}^{}{P}_i}{X}_i$

$\begin{array}{l}=\frac{1}{2}*1+\frac{1}{3}*2+\frac{1}{6}*5\\ =\frac{1}{2}+\frac{2}{3}+\frac{5}{6}\\ =\frac{3+4+5}{6}\\ =\frac{12}{6}\\ =2\end{array}$

Therefore, option (B) is correct.

64. It is given that P (X = 0) = 30% = 30/100 = 0.3

P (X = 1) = 70% = 70/100 = 0.7

Therefore, the probability distribution is as follows.

$\begin{array}{l}Then,E\left(X\right)={\displaystyle \sum _{}^{}{X}_{i}P}\left(X_i\right)\\ =0*0.3+1*0.7\\ =0.7\end{array}$

$\begin{array}{l}E\left(X^2\right)={\displaystyle \sum _{}^{}{X^2}_{i}P}\left(X_i\right)\\ =0^2*0.3+{\left(1\right)}^2*0.7\\ =0.7\end{array}$

It is know that,  $Var\left(X\right)=E\left(X^2\right)-{\left[E\left(X\right)\right]}^2$

= 0.7 − (0.7)²

= 0.7 − 0.49

= 0.21

63. There are 15 students in the class. Each student has the same chance to be chosen. Therefore, the probability of each student to be selected is 1/15.

The given information can be compiled in the frequency table as follows.

P(X = 14) =2/15, P(X = 15) =1/15, P(X = 16) =2/15, P(X = 16) =3/15,

P(X = 18) =115, P(X = 19) =2/15, P(X = 20) =3/15, P(X = 21) =1/15

Therefore, the probability distribution of random variable X is as follows.

Then, mean of X = E(X)

$\begin{array}{l}={\displaystyle \sum _{}^{}{X}_{i}P}\left(X_i\right)\\ =14*\frac{2}{15}+15*\frac{1}{15}+16*\frac{2}{15}+17*\frac{3}{15}+18*\frac{1}{15}+19*\frac{2}{15}+20*\frac{3}{15}+21*\frac{1}{15}\\ =\frac{1}{15}\left(28+15+32+51+18+38+60+21\right)\\ =\frac{263}{15}\\ =17.53\end{array}$

$\begin{array}{l}E\left(X^2\right)={\displaystyle \sum _{}^{}{X^2}_{i}P}\left(X_i\right)\\ ={\left(14\right)}^2.\frac{2}{15}+{\left(15\right)}^2.\frac{1}{15}+{\left(16\right)}^2.\frac{2}{15}+{\left(17\right)}^2.\frac{3}{15}+{\left(18\right)}^2.\frac{1}{15}+{\left(19\right)}^2.\frac{2}{15}+{\left(20\right)}^2.\frac{3}{15}+{\left(21\right)}^2.\frac{1}{15}\\ =\frac{1}{15}.\left(392+225+512+867+324+722+1200+441\right)\\ =\frac{4683}{15}\\ =312.2\end{array}$

$\begin{array}{l}\therefore Variance\left(X\right)=E\left(X^2\right)-{\left[E\left(X\right)\right]}^2\\ =312.2-{\left(\frac{263}{15}\right)}^2\\ =312.2-307.4177\\ =4.7823\\ \approx 4.78\end{array}$

Standard derivation $\begin{array}{l}=\surd variance\; (X)\\ =\surd 4.78\\ =2.186\approx 2.19\end{array}$