Probability

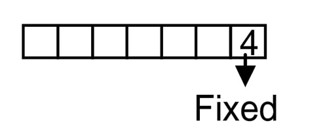
3, 4, 5, 5

In remaining six places you have to arrange

3, 4, 5,5

So no. of ways $=\frac{6!}{2!2!2!}$  

Total no. of seven digits nos. = $\frac{7!}{2!3!2!}*1$  

Hence Req. prob. $\frac{\frac{6!}{2!2!2!}}{\frac{7!}{2!3!2!}}=\frac{6!3!}{2!7!}=\frac{3}{7}$

f (x) = x? – 4x + 1 = 0
f' (x) = 4x³ – 4
= 4 (x–1) (x²+1+x)
=> Two solution

$\tilde{z}=i{z}^2+z^2-z$

$z+\overline{Z}=z^2\left(i+1\right)$

$z+\overline{Z}=z^2\left(i+1\right)$ Let z be equal to (x + iy)

(x + iy) + (x – iy) = (x + iy)² (i + 1)

$2x=\left(x^2-y^2+2ixy\right)\left(i+1\right)$               

Equating the real & in eg part.

$\left(x^2-y^2+2ixy\right)=0.........\left(i\right)$

$\left(x^2-y^2-2xy\right)=\left(2x\right)..............\left(ii\right)$               

(i) & (ii)

 4xy = -2x Þ x = 0 or y = $\left(\frac{-1}{2}\right)$  

(for x = 0, y = 0)

For y = $\frac{-1}{2}$  

x²   $-\frac{1}{4}+2\left(\frac{-1}{2}\right)x=0$

x =   $\frac{4\pm \sqrt[]{16+16}}{2.4}$

=  $\left(\frac{1+\sqrt[]{2}}{2}\right)or\left(\frac{1-\sqrt[]{2}}{2}\right)$  

$\therefore sum$ of   ${\left|z\right|}^2={\left(\frac{1+\sqrt[]{2}}{2}\right)}^2+\frac{1}{4}+{\left(\frac{1-\sqrt[]{2}}{2}\right)}^2+\frac{1}{4}+0^2+O^2$

=   $\frac{3}{4}+\frac{\sqrt[]{2}}{2}+\frac{1}{4}+\frac{3}{4}-\frac{\sqrt[]{2}}{2}+\frac{1}{4}=\frac{3}{2}+\frac{1}{2}=2$

 $\frac{dy}{dx}=\frac{1}{1+sin2x}$

$dy=\frac{se{c}^{2}xdx}{{\left(1+tanx\right)}^2}$

$\Rightarrow y=-\frac{1}{1+tanx}+c$

When

$x=\frac{\pi }{4},y=\frac{1}{2}$ gives c = 1

So

$x+\frac{\pi }{4}=\frac{5\pi }{6}or\frac{13\pi }{6}\Rightarrow x=\frac{7\pi }{12}or\frac{23\pi }{12}$

sum of all solutions =

$\pi +\frac{7\pi }{12}+\frac{23\pi }{12}=\frac{42\pi }{12}$

Hence k = 42

Each element of ordered pair (i, j) is either present in A or in B.

So, A + B = Sum of all elements of all ordered pairs {i, j} for $1\le i\le 10$ and $1\le j\le 10$

= 20 (1 + 2 + 3 + … + 10) = 1100

$\frac{24}{\pi }{\displaystyle \underset{0}{\overset{\sqrt[]{2}}{\int }}\frac{\left(2-x^2\right)}{\left(x^2+2\right)\sqrt[]{4+x^4}}dx}$

$\frac{24}{\pi }{\displaystyle \underset{0}{\overset{\sqrt[]{2}}{\int }}\frac{x^2\left(\frac{2}{x^2}-1\right)dx}{x\left(x+\frac{2}{x}\right)*x\sqrt[]{\frac{4}{x^2}+x^2}}}$

$x+\frac{2}{x}=t$

$dt=\left(1-\frac{2}{x^2}\right)dx$

$=-\frac{12}{\pi }\left[\frac{\pi }{4}-\frac{2\pi }{2*2}\right]=-\frac{12}{\pi }\left[-\frac{\pi }{4}\right]=3$