Probability
Get insights from 66 questions on Probability, answered by students, alumni, and experts. You may also ask and answer any question you like about Probability
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
47. Since the die has two faces each mark 1, three faces each marks 2 and one face mark 3.
The possible sample space of outcome is.
S = {1, 2, 3} so, n (s) = 6
(i) P (2)
(ii) P (1 or 3) = P (1) + P (3) =
(iii) P (not 3) = 1 P (3) = 1 - =
New answer posted
7 months agoContributor-Level 10
46. Total number of ways of drawing 4 cards from a duck of 52 cards, n (s) = 52C4
Total no. of diamond cards = 13
Similarly, total. no. of spades cards = 13

New answer posted
7 months agoContributor-Level 10
45. Given,
No. of red marbles= 10
No. of blue marbles = 20
No. of green marbles = 30.
So, total no. of marbles = 10 + 20 + 30 = 60
Now, we are to select 5 marbles from the given 60 marbles.
So the sample space is:
n (s) = 60c5.
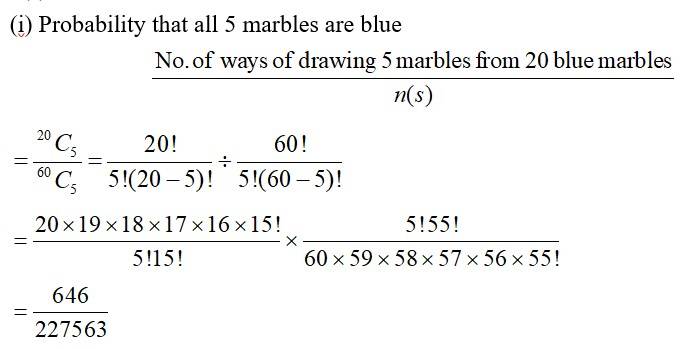

New answer posted
7 months agoContributor-Level 10
44. Given that, total number of student, n (S) = 60
Let A: student opted for NCC
n (A) = 30
B: student opted for NSS
n (B) = 32
And student who opted both NCC and NSS, n (A∩B) = 24
(i) Probability that student opted for NCC or NSS,
P (A∪B) = P (A) + P (B) – P (A∩B)
(ii) Probability that student opted neither NCC or NSS
P (not A and not B) = P (A'∩B') = P (A∪B)' = 1 – P (A∪B)
(iii) Probabilities that student opted NSS but not NCC
P (B but not A) = P (B) – P (A∩B)
New answer posted
7 months agoContributor-Level 10
43. Let A: student passing in Hindi
B: student passing in English
Given, P (B) = 0.75
P (A∩B) = 0.5, passing both subject
And P (A'∩B') = 0.1, i.e., passing neither subject
P (A∪B)' = 0.1
1 – P (A∪B) = 0.1
P (A∪B) = 1 – 0.1
P (A∪B) = 0.9
Hence, P (A∪B) = P (A) + P (B) – P (A∩B)
P (A) = P (A∪B) + P (A∩B) – P (B)
P (A) = 0.9 + 0.5 – 0.75 = 0.65
? The probability of passing Hindi examination is 0.65.
New answer posted
7 months agoContributor-Level 10
42. Let A: Student passes 1st examination
So, P (A) = 0.8
And B: Student passes 2nd examination
So, P (B) = 0.7
Also probability of passing at least one examination is P (A∪B) = 0.95
Therefore, P (A∪B) = P (A) + P (B) – P (A∩B)
0.95 = 0.8 + 0.7 – P (A∩B)
P (A∩B) = 0.8 + 0.7 – 0.95
P (A∩B) = 0.55
Hence, probability of passing both examination is 0.55.
New answer posted
7 months agoContributor-Level 10
41. Given that, 40% study Mathematics, 30% study Biology and 10% study both Mathematics and Biology.
Let A: Students study Mathematics.
P (A) = 40% = .
Let B: Students study Biology.
P (B) = 30% = .
So, P (A∩B) i.e. probability of student studying both Mathematics and Biology is
P (A∩B) = 10% =
? P (A∪B); probability of student studying Mathematics or Biology is
P (A∪B) = P (A) + P (B) – P (A∩B)
.
New answer posted
7 months agoContributor-Level 10
40. Given P (A) = 0.42
P (B) = 0.48
P (A∩B) = 0.16
(i) P (not A) = P (A') = 1 – P (A) = 1 – 0.42 = 0.58
(ii) P (not B) = P (B') = 1 – P (B) = 1 – 0.48 = 0.52
(iii) P (A or B) = P (A∪B) = P (A) + P (B) – P (A∩B)
= 0.42 + 0.48 – 0.16
= 0.74
New answer posted
7 months agoContributor-Level 10
39. Given, P (not E or not F) = 0.25
P (E'∪F') = 0.25
P (E∩F)' = 0.25
1 – P (E∩F) = 0.25
P (E∩F) = 1 – 0.25
P (E∩F) = 0.75≠ 0
Hence, E and F are not mutually exclusive events.
New answer posted
7 months agoContributor-Level 10
38. Given, P (E) =
P (F) =
P (E and F) = P (E∩F) =
(i) P (E or F) = P (E∪F) = P (E) + P (F) – P (E∩F)
(ii) P (not E and not F) = P (E'∩F') = P (E∪F)' = 1 – P (E∪F)
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers
