Class 11th
Get insights from 8k questions on Class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
5 months agoContributor-Level 10
Let the equation of circle be
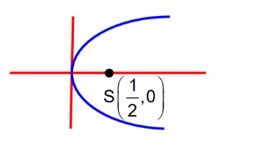
Radius =
This circle and parabola
touch each other, so
New answer posted
5 months agoContributor-Level 10
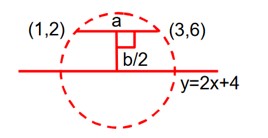
As slope of line joining (1, 2) and (3, 6) is 2 given diameter is parallel to side
New answer posted
5 months agoNew answer posted
5 months agoContributor-Level 10
for
->r = 24
k = 3 + exponent of 5 in 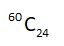
=
= 3 + (12 + 2 – 4 – 0 – 7 – 1)
= 3 + 2 = 5
New answer posted
5 months agoContributor-Level 10
For an acid- base titration, Methly orange exist at end point as quinonoid form.
New answer posted
5 months agoContributor-Level 10
The two main types of potential energy are:
- Gravitational Potential Energy - Energy stored due to an object's position in a gravitational field (PE = mgh).
- Elastic Potential Energy - Energy stored in deformed elastic objects like springs or stretched materials (PE = ½kx²).
New answer posted
5 months agoContributor-Level 10
The best way to find potential energy is to use the relationship
and integrating the conservative force over the path.
For common cases, apply the standard potential energy formulas:
- PE = mgh for gravity
- PE = ½kx² for springs.
New answer posted
5 months agoContributor-Level 10
Potential energy is best defined as a stored energy in a system. This energy is stored due to the configuration or position of the objects within a conservative force field. Potential energy in physics tells us that it's the capacity of the work done when the system is allowed to move from that position to the reference point.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers