Class 11th
Get insights from 8k questions on Class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
8 months agoContributor-Level 10
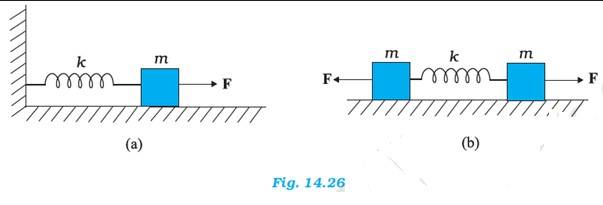
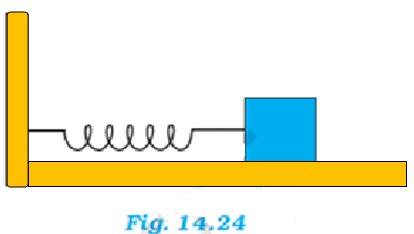
(a) For figure (a) : When a force F is applied to the free end of the spring, an extension l is produced. For the maximum extension, it can be written as:
F – kl, where k is the spring constant.
For maximum =extension of the spring, l =
For figure (b): The displacement (x) produced in this case is x =
Net force F = +2kx = 2k . So l =
(b) For figure (a) : For mass (m) of the block, force is written as : F = ma = m ,
where x is the displacement of the block in time t, then
m , it is negative because the direction of the elastic force is opposite to the direction of displacement.
=&
New answer posted
8 months agoContributor-Level 10
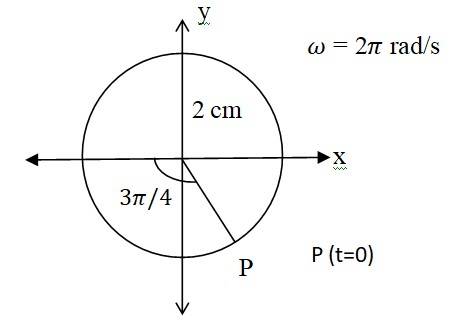
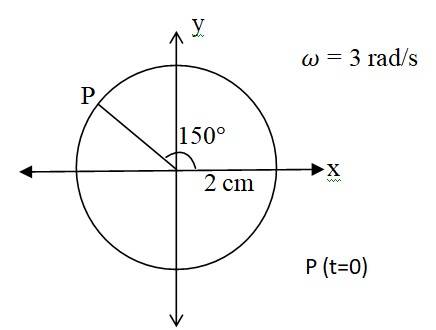
(a) X = -2 sin( 3t + ) = +2cos ( 3t + + = 2 cos (3t + )
when we compare this equation with standard SHM equation
x = Acos ( t + ), then we get
Amplitude A = 2 cm. Phase angle = 150 , angular velocity = 3 rad/s
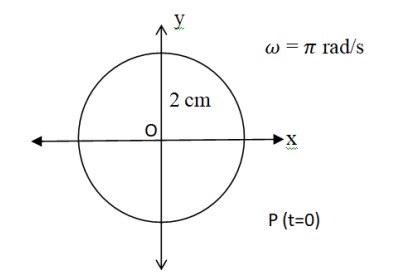
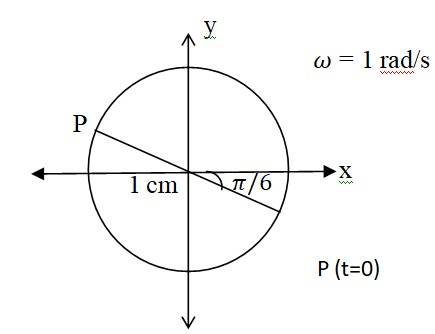
(b) X= cos ( t) = cos ( )
when we compare this equation with standard SHM equation
x = Acos( t + ), then we get
Amplitude A = 1 cm. Phase angle = - 30 , angular velocity = 1 rad/s
(c) X = 3sin (2 t + ) = -3cos
when we compare this equation w
New answer posted
8 months agoContributor-Level 10
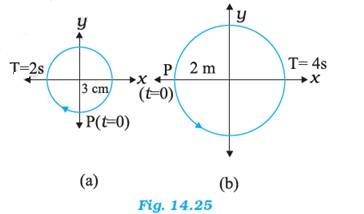
(a) Time period, T = 2 s, Amplitude A = 3 cm
At time, t = 0, the radius vector makes an angle with the positive x-axis, i.e. phase angle = +
Therefore, the equation of simple harmonic motion for the x-projection of the radius vector, at time t is given by the displacement equation:
x = Acos = 3cos = -3sin ( ) = -3sin cm
(b) Time period, T = 4 s, Amplitude A = 2 m
At time, t = 0, the radius vector makes an angle with the positive x-axis, i.e. phase angle = +
Therefore, the equation of simple harmonic motion for the x-projection of the r
New answer posted
8 months agoContributor-Level 10
The functions have the same frequency and amplitude, but different initial phases.
Distance travelled by the mass sideways, A = 2.0 cm
Force constant of the spring, k = 1200 N/m and mass, m = 3 kg
Angular frequency, = = 20 rad/s
(a) When mass is at the mean position, displacement x = Asin cm
(b) At the maximum stretched position, the mass is towards extreme right. Hence the initial phase is
x = A sin ( = 2sin (20t + = 2cos20t
(c) At the maximum compressed position, the mass is towards the extreme left
Hence, the initial phase is
x = Asin ( = 2 cos20t
Hence, the f
New answer posted
8 months agoContributor-Level 10
Spring constant, k = 1200 N/m
Mass, m = 3 kg
Displacement, d = 2 cm = 0.02 m
(a) Frequency of oscillation, v is given by
v = = = = 3.183 m/s
(b) Maximum acceleration (a) is given by the relation: a =
where, angular frequency = and A = maximum displacement
a = = = 8 m/
(c) Maximum velocity, = = 0.4 m/s
Hence the maximum velocity of the mass is 0.4 m/s
New answer posted
8 months agoContributor-Level 10
The maximum mass that the scale can read, M = 50 kg
Maximum displacement of the spring = Length of the scale, l = 20 cm = 0.2 m
Time period, T = 0.6 s
Maximum force exerted on the spring, F =Mg
g = acceleration due to gravity = 9.8 m/
Hence, F = 50 = 490 N
Spring constant k = = = 2450 N/
Mass m is suspended from the balance, hence time period, T =
m = ( = ( = 22.34 kg
Weight = mg = 218.944 N
So the weight of the body is about 219 kg.
New answer posted
8 months agoContributor-Level 10
Initially at t =0, Displacement, x = 1 cm
Initial velocity, v = cm/s, Angular frequency, = rad/s
It is given that: x(t) = A cos ( t + )
Then 1 = A cos (
A cos = 1 ….(i)
Velocity, v =
1 = -Asin(
Asin ………(ii)
Squaring and adding equations (i) and (ii), we get
= 1+1
A = cm
= -1
Then = , ,,,
SHM is given as X = Bsin( t + )
Putting the given values in this equation, we get
1 = Bsin( )
Bsin =1…….(iii)
Velocity V = Bcos( t + &nbs
New answer posted
8 months agoContributor-Level 10
A motion represents simple harmonic motion if it is governed by the force of law
F = ma, where F is the force, m is the mass and a is the acceleration and F = kx, where k is a constant among given equation and x is the displacement.
We can write a = x
Only equation a = -10x is written in this form. Hence this relation represents SHM. The answer is option (c).
New answer posted
8 months agoContributor-Level 10
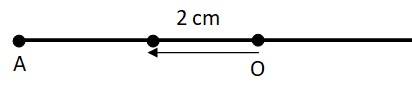
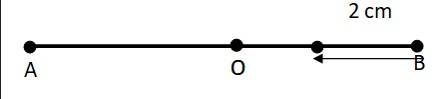
a)

The given situation is shown in the figure. Points A and B are the two end points, with AB = 10 cm. O is the midpoint of the path. A particle is in linear simple harmonic motion between the end points. At the extreme point A, the particle is at rest momentarily. Hence, its velocity is zero at this point. Its acceleration is positive as it is directed along AO. Force is also positive in this case as the particle is directed rightward.
(b) At the extreme point B, the particle is at rest momentarily. Hence, its velocity is zero at this point. Its acceleration is negative in this case as it is directed along B. Force is also
New answer posted
8 months agoContributor-Level 10
(a) The given function is sin t – cos t
= =
= )
This function represents SHM as it can be written in the form: a sin ( t + )
Its period is . It is periodic, but not SHM
(b) Sin3 t =
The terms t and t individually represents simple harmonic motion. However, the superposition of two SHM is periodic but not simple harmonic.
(c) The given function is 3 cos ( /4 – 2 t) = -3cos(2 t - /4)
This function represents simple harmonic motion because it can be written in the form: a cos(
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 684k Reviews
- 1800k Answers