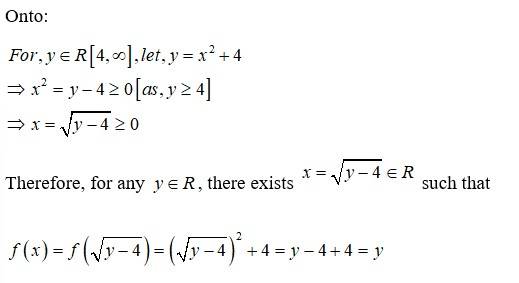Class 12th
Get insights from 11.8k questions on Class 12th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 12th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
8 months agoContributor-Level 10
(i) On Z, * is defined by a * b = a − b.
It can be observed that 1 * 2 = 1 − 2 = 1 and 2 * 1 = 2 − 1 = 1.
∴1 * 2 ≠ 2 * 1; where 1, 2 ∈ Z
Hence, the operation * is not commutative.
Also we have:
(1 * 2) * 3 = (1 − 2) * 3 = −1 * 3 = −1 − 3 = −4
1 * (2 * 3) = 1 * (2 − 3) = 1 * −1 = 1 − (−1) = 2
∴(1 * 2) * 3 ≠ 1 * (2 * 3) ; where 1, 2, 3 ∈ Z
Hence, the operation * is not associative.
(ii) On Q, * is defined by a * b = ab + 1.
It is known that:
ab = ba & mn For E; a, b ∈ Q
⇒ ab + 1 = ba&nb
New answer posted
8 months agoContributor-Level 10
(i) On Z+, * is defined by a * b = a − b.
It is not a binary operation as the image of (1, 2) under * is 1 * 2 = 1 − 2= −1 ∉ Z+.
(ii) On Z+, * is defined by a * b = ab.
It is seen that for each a, b ∈ Z+, there is a unique element ab in Z+.
This means that * carries each pair (a, b) to a unique element a * b = ab in Z+.
Therefore, * is a binary operation.
(iii) On R, * is defined by a * b = ab2.
It is seen that for each a, b ∈ R, there is a unique element ab2 in R.
This means that * carries each pair (a, b) to a unique element a * b = ab2 in R.
Therefore, * is a binary operation.
(iv) On Z+, * is defined by a * b = |a −
New answer posted
8 months agoContributor-Level 10
It is given that is defined as
Let y be an arbitrary element of Range f.
Then, there exists such that
let us define g: Range
Thus, g is the inverse of f i.e.,
Hence, the inverse of f is the map g: Range which is given by
The correct answer is B.
New answer posted
8 months agoContributor-Level 10
Let f: X → Y be an invertible function.
Then, there exists a function g: Y → X such that gof = IX and fog = IY.
Here, f−1 = g.
Now, gof = IX and fog = IY
⇒ f−1 of = IX and fof−1 = IY
Hence, f−1 : Y → X is invertible and f is the inverse of f−1
i.e., (f−1)−1 = f.
New answer posted
8 months agoContributor-Level 10
If we define then we have:
Thus, the inverse of f exists and
is given by,
Let us now find the inverse of i.e., find the inverse of g.
If we define
, then we have
Thus, the inverse of g exists and
It can be noted that h=f.
Hence,
New answer posted
8 months agoContributor-Level 10
Let be an invertible function.
Also, suppose f has two inverses (say g1 and g2 ).
Then, for all y ∈ Y, we have:
[f is invertible => f is one-one]
[g is one-one]
Hence, f has a unique inverse.
New answer posted
8 months agoContributor-Level 10
is given by,
f is a one-one function.
Onto:
Therefore, for any , there exists such that
f is onto.
Thus, f is one-one and onto and therefore, exists.
Let us define by
Hence, f is invertible and the inverse of f is given by
New answer posted
8 months agoContributor-Level 10
is given as
f is a one-one function.
It is clear that Range f is onto.
Range f is one-one onto and therefore, the inverse of the function:
Range f exists.
Let g: Range be the inverse of f.
Let y be an arbitrary element of range f.
Since Range f is onto, we have:
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 685k Reviews
- 1800k Answers