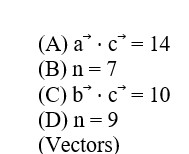Class 12th

The relationship between the de Broglie wavelengths of an electron (λe) and a photon (λp) is derived as follows:
For an electron: λe = h / mv = h / √ (2mE)
For a photon: λp = h / p = hc / E

Taking the ratio of the wavelengths squared:
(λe / λp)² = [h / √ (2mE)]² / [hc / E]²
(λe / λp)² = (h² / 2mE) * (E² / h²c²)
(λe / λp)² = E / 2mc²
(λe / λp) = (1/c) * √ (E / 2m)

Given:

• i = 10
• e = 1.6 x 10? ¹? C
• A = 5 x 10?
• V = 2 x 10? ³

The formula for current is I = neAV.
Rearranging for n (number of free electrons per unit volume):
n = I / (eAV)
n = 10 / (1.6 * 10? ¹? * 5 * 10? * 2 * 10? ³)
n = 625 * 10²?

Hormones present in the human body are:

• Thyrotropin-releasing hormone (TRH)

• Dopamine (prolactin-inhibiting hormones)

• Gonadotropin-releasing hormone (GnRH)

• Adrenal Glands

• Androgens

• Estrogen

• Inhibin

• Testosterone

• Gastrin

• Melatonin

P (at least 2 show 3 or 5) =? C? (2/6)² (4/6)² +? C? (2/6)³ (4/6)¹ +? C? (2/6)?
= (384+128+16)/6? = 11/27
n=27
∴ expectation of number of times = np
= 27 ⋅ (11/27) = 11

Below is the list of hormones:

1. Cortisol
2. Estrogen & Progesterone
3. Aldosterone 
4. Insulin
5. Growth Hormone
6. Glucagon
7. Adrenaline (Epinephrine)
8. Thyroxine (T4) and Triiodothyronine (T3)
9. Melatonin

We have, 1 - (probability of all shots result in failure) > 1/4
? 1 - (9/10)? > 1/4
? 3/4 > (9/10)? ? n? 3 > (9/10)? ? n? 3

-5 ≤ [x/2] < 5
I ⇒ [x/2] = -5, -4, -3, -2, -1,0,1,2,3,4
Hence, function is discontinues at = -4, -3, -2, -1,1,2,3,4 Number of values is 8.

-5? [x/2] < 5
I? [x/2] = -5, -4, -3, -2, -1,0,1,2,3,4
Hence, function is discontinues at = -4, -3, -2, -1,1,2,3,4 Number of values is 8.

Volume of parallelepiped v = | [a? b? c? ]|
v = | 1 n |
| 2 4 -n| = ±158
| 1 n 3 |
1 (12+n²) - 1 (6+n) + n (2n-4) = ±158
3n²-5n+152=0 or 3n²-5n+164=0
D<0 (no real roots)
n=8, -19/3 ⇒ n=8
then b? ⋅c? = 2+4n-3n=10
a? ⋅c? = 1+n+3n=33