Class 12th
Get insights from 12k questions on Class 12th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 12th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
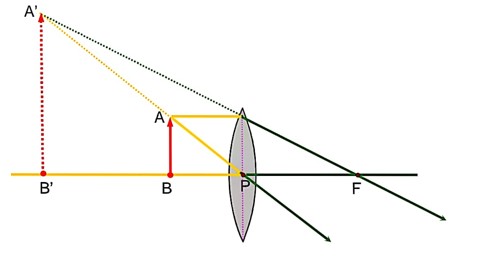
3 months agoContributor-Level 10
l + m – n = 0
l + m = n . (i)
l2 + m2 = n2
Now from (i)
l2 + m2 = (l + m)2
=> 2lm = 0
=>lm = 0
l = 0 or m = 0
=> m = n Þ l = n
if we take direction consine of line
cos a =
![]()
New answer posted
3 months agoContributor-Level 10
With the help of conservation of linear momentum, we can write
New answer posted
3 months agoContributor-Level 10
xyz = 24
24 = 23 * 3
Let's distribute 2, 3 among 3 variables. No. of positive integral solution =
No. of ways to distribute =
New answer posted
3 months agoContributor-Level 10
x + y =
h = y . (ii)
(i) & (ii) x + y =
Let the speed be S
x = 20.S
from (iii)
New answer posted
3 months agoContributor-Level 10
(2 – i) z = (2 + i) , put z = x + iy
(ii)
x + 2y = 2
(iii)
Equation of tangent x – y + 1 = 0
Solving (i) and (ii)
Perpendicular distance of point from x – y + 1 = 0 is p = r
New answer posted
3 months agoContributor-Level 10
Let
A : Missile hit the target
B : Missile intercepted
P (B) =
Required Probability =
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers