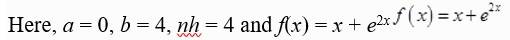Class 12th

This is a Multiple Choice Questions as classified in NCERT Exemplar

Answer – (a, d)

Explanation – magnetic field lines for magnetic induction B form continuous lines. So lines of B are necessarily continuous across S.

Also H varies inside and outside. So lines of H cannot all be continuous across S

This is a Multiple Choice Questions as classified in NCERT Exemplar

Answer- (b)

Explanation- as curie law explains B $\propto \frac{\mathit{B}\left(\mathit{m}\mathit{a}\mathit{g}\mathit{n}\mathit{e}\mathit{t}\mathit{i}\mathit{c}\mathit{}\mathit{f}\mathit{i}\mathit{e}\mathit{l}\mathit{d}\mathit{}\mathit{i}\mathit{n}\mathit{d}\mathit{u}\mathit{c}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\right)}{\mathit{t}\left(\mathit{t}\mathit{e}\mathit{m}\mathit{p}\mathit{}\mathit{i}\mathit{n}\mathit{}\mathit{k}\mathit{e}\mathit{l}\mathit{v}\mathit{i}\mathit{n}\right)}$

$\frac{I_2}{I_1}=\frac{B_2}{B_1}*\frac{t_1}{t_2}$

_{$I$ 1} =8Am^-1, B₁= 0.6T, t₁=4K

B₂= 0.2T, t₂=16K

So after solving we get I₂= 2/3Am^-

$\begin{array}{l}{\displaystyle {\int }_{-1}^1\left(x+1\right)dx}={\displaystyle {\int }_{-1}^1.xdx+{\displaystyle {\int }_{-1}^{1}dx}}\\ ={\left[\frac{x^2}{2}\right]}_{-1}^1+{\left[x\right]}_{-1}^1\\ =\left[\frac{1^2}{2}-\frac{{\left(-1\right)}^2}{2}\right]+\left[1-\left(-1\right)\right].\\ =\left[\frac{1}{2}-\frac{1}{2}\right]+\left[1+1\right]=2.\end{array}$

We know that  ${\displaystyle \underset{a}{\overset{b}{\int }}f\left(x\right)dx}=\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}h\left[f\left(a\right)+f\left(a+h\right)+f\left(a+2h\right)+......+f\left(a+\left(n-1\right)h\right)\right]$

where nh = b - a

$\begin{array}{l}\therefore {\displaystyle \underset{0}{\overset{4}{\int }}\left(x+e^{2x}\right)dx}=\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}h\left[1+\left(h+e^{2h}\right)+\left(2h+e^{4h}\right)+......+\left(\left(n-1\right)h+e^{2\left(n-1\right)h}\right)\right]\\ =\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}h\left[\left(h+2h+......+\left(n-1\right)h\right)+\left(1+e^{2h}+e^{4h}+......+e^{2\left(n-1\right)h}\right)\right]\\ =\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}h\left[h\left(1+2+......+\left(n-1\right)\right)+a\left(\frac{r^n-1}{r-1}\right)\right]\end{array}$

$=\underset{\begin{array}{l}h\to 0\\ h\to \infty \end{array}}{lim}\left[h.h\frac{n\left(n-1\right)}{2}+\frac{1\left({\left(e^{2n}\right)}^n-1\right)}{e^{2h}-1}\right]$

$\begin{array}{l}=\underset{\begin{array}{l}h\to 0\\ h\to \infty \end{array}}{lim}\left[\frac{nh\left(nh-h\right)}{2}+\frac{h\left({\left(e^{2nh}\right)}^n-1\right)}{e^{2h}-1}\right]\\ =\underset{\begin{array}{l}h\to 0\\ h\to \infty \end{array}}{lim}\left[\frac{4\left(4-h\right)}{2}+\frac{h\left(\left(e^{24}\right)-1\right)}{e^{2h}-1}\right]\\ =\left[\frac{4\left(4-0\right)}{2}+\left(e^8-1\right)\underset{h\to 0}{lim}\frac{h}{e^{2h}-1}\right]\\ =8+\left(e^8-1\right)\frac{1}{2}\underset{h\to 0}{lim}\frac{2h}{e^{2h}-1}\\ =8+\frac{\left(e^8-1\right)}{2}=\frac{e^8-15}{2}\\ \left[?\underset{x\to 0}{lim}\frac{x}{e^x-1}=1\right]\end{array}$

We know that  ${\displaystyle \underset{a}{\overset{b}{\int }}f\left(x\right)dx}=\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}h\left[f\left(a\right)+f\left(a+h\right)+f\left(a+2h\right)+......+f\left(a+\left(n-1\right)h\right)\right]$

where nh = b - a

Here, a = -1, b = 1, nh = 2 and f(x) = e^x

$\therefore {\displaystyle \underset{-1}{\overset{4}{\int }}{e}^{x}dx}=\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}h\left[e^{-1}+e^{-1}e+e^{-1}{e}^{2h}+......+e^{-1}{e}^{\left(n-1\right)h}\right]=\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}h{e}^{-1}\frac{\left[{\left(e^h\right)}^n-1\right]}{e^h-1}$

[ $?$  The series within brackets is a G.P. and  $S_n=a\frac{r^n-1}{r-1}$ ]

$\begin{array}{l}=\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}he\frac{\left(e^{nh}-1\right)}{e^h-1}\\ =\underset{h\to 0}{lim}h{e}^{-1}\frac{\left(e^2-1\right)}{e^h-1}\\ =e^{-1}\left(e^2-1\right)\underset{h\to 0}{lim}\frac{h}{e^h-1}\\ =e^{-1}\left(e^2-1\right)*1\left[?\underset{x\to 0}{lim}\frac{x}{e^x-1}=1\right]\\ =e^{-1+2}-e^{-1}=e-e^{-1}=e-\frac{1}{e}\end{array}$

This is a Multiple Choice Questions as classified in NCERT Exemplar

Answer- (b)

Explanation- as gauss's law states $\int E.ds$ = q/ $?$ ₀ for electrostatic field. It does not contradicts for electrostatic fields as the electric field lines do not form continuous closed path

According to gauss's law in magnetic field

$\int E.ds$ =0

It contradicts for magnetic field, because there is a magnetic field inside the solenoid and no field outsid the solenoid carrying current but the magnetic field lines from the closed path.

We know that  ${\displaystyle \underset{a}{\overset{b}{\int }}f\left(x\right)dx}=\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}h\left[f\left(a\right)+f\left(a+h\right)+f\left(a+2h\right)+......+f\left(a+\left(n-1\right)h\right)\right]$

where nh = b - a

Here, a = 1, b = 4, nh = 3 and f(x) = x² - xf(x) =  x² - x 

$\begin{array}{l}\therefore {\displaystyle \underset{1}{\overset{4}{\int }}\left(x^2+x\right)dx}=\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}h\left[0+h+h+2h+4h^2+......+\left(n-1\right)h+{\left(n-1\right)}^2{h}^2\right]\\ =\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}h\left[h\left(1+2+3+......+\left(n-1\right)\right)+h^2\left(1^2+2^2+......{\left(n-1\right)}^2\right)\right]\\ =\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}h\left[4nh+4hh\frac{n\left(n-1\right)}{2}+hhh\frac{n\left(n-1\right)\left(2n-1\right)}{6}\right]\\ =\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}h\left[h\left(1+2+3+......+\left(n-1\right)\right)+h^2\left(1^2+2^2+......{\left(n-1\right)}^2\right)\right]\\ =\underset{h\to 0}{lim}h\left[3\frac{\left(3-h\right)}{2}+\frac{3\left(3-h\right)\left(2.3-h\right)}{6}\right]\\ =\left[3\frac{\left(3-0\right)}{2}+\frac{3\left(3-0\right)\left(6-0\right)}{6}\right]\\ =\left[\frac{9}{2}+9\right]=\frac{27}{2}\end{array}$

This is a Multiple Choice Questions as classified in NCERT Exemplar

Answer- (d)

Explanation- the individual atoms in a ferromagnetic material possess dipole moment as in a paramagnetic material.

However they interact with one another in such a way that they spontaneously align themselves in a common direction over a microscopic volumes called domain. Thus they align perfectly.

We know that  ${\displaystyle \underset{a}{\overset{b}{\int }}f\left(x\right)dx}=\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}h\left[f\left(a\right)+f\left(a+h\right)+f\left(a+2h\right)+......+f\left(a+\left(n-1\right)h\right)\right]$

where nh = b - a

Here, a = 2, b = 3, nh = 1 and f(x) = x²

$\begin{array}{l}\therefore {\displaystyle \underset{a}{\overset{b}{\int }}{x}^{2}dx}=\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}h\left[4+\left(4+4h+h^2\right)+\left(4+8h+2^2{h}^2\right)+......+\left(4+4\left(n-1\right)h+{\left(n-1\right)}^2{h}^2\right)\right]\\ =\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}h\left[4n+4h+\left(1+2+3+......+\left(n-1\right)\right)+h^2\left(1^2+2^2+......{\left(n-1\right)}^2\right)\right]\\ =\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}h\left[4nh+4hh\frac{n\left(n-1\right)}{2}+hhh\frac{n\left(n-1\right)\left(2n-1\right)}{6}\right]\\ =\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}h\left[4nh+4hh\frac{\left(nh-h\right)}{2}+\frac{nh\left(nh-h\right)\left(2nh-h\right)}{6}\right]\end{array}$

$\begin{array}{l}=\underset{h\to 0}{lim}h\left[4+2\left(1-h\right)+\frac{\left(1-h\right)\left(2-h\right)}{6}\right]\\ =\left[4+2\left(1-0\right)+\frac{\left(1-0\right)\left(2-0\right)}{6}\right]\\ =6+\frac{1}{3}=\frac{19}{3}\end{array}$

We know that  ${\displaystyle \underset{a}{\overset{b}{\int }}f\left(x\right)dx}=\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}h\left[f\left(a\right)+f\left(a+h\right)+f\left(a+2h\right)+......+f\left(a+\left(n-1\right)h\right)\right]$

where nh = b - a

Here, a = 0, b = 5, nh = 5 and f(x) = x + 1

$\begin{array}{l}\therefore {\displaystyle \underset{0}{\overset{5}{\int }}\left(x+1\right)dx=\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}h\left[1+\left(h+1\right)+\left(2h+1\right)+.....+\left(\left(n-1\right)h+1\right)\right]}\\ \Rightarrow {\displaystyle \underset{0}{\overset{5}{\int }}\left(x+1\right)dx=\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}h\left[n+h\left(1+2+3.....+\left(n-1\right)\right)\right]}\\ \Rightarrow {\displaystyle \underset{0}{\overset{5}{\int }}\left(x+1\right)dx=\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}h\left[nh+h\frac{n\left(n-1\right)}{2}\right]}\\ =\underset{\begin{array}{l}h\to 0\\ n\to \infty \end{array}}{lim}\left[nh+\frac{nh\left(nh-h\right)}{2}\right]\end{array}$

$\begin{array}{l}=\underset{h\to 0}{lim}\left[5+\frac{5\left(5-h\right)}{2}\right]\\ =\left[5+\frac{5\left(5-0\right)}{2}\right]\\ =5+\frac{25}{2}=\frac{35}{2}\end{array}$