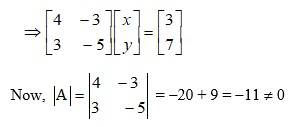Class 12th
Get insights from 12k questions on Class 12th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 12th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoNew answer posted
7 months agoContributor-Level 10
The given system of eqn in matrix form is AK = B.
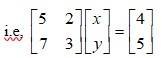
Then, |A| = 5 x 3 - 7 x 2 = 15 - 14 = 1 ≠ 0
∴ The system has a unique solution.
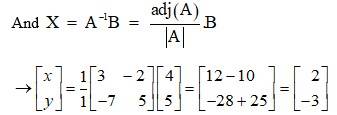
∴ k = 2 and y = -3
New answer posted
7 months agoContributor-Level 10
The given system of eqn in matrix form is AK = B
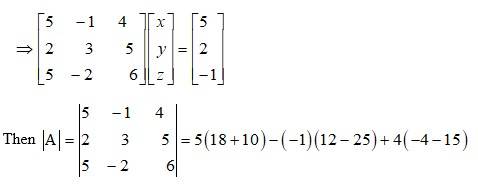
= 5 x 28 -13 + 4 x (-9)
= 140 - 13 - 76
= 51 ≠ 0 .
The given system of eqn are consistent
New answer posted
7 months agoContributor-Level 10
The given system of eqn using matrix form can be written as AK = B
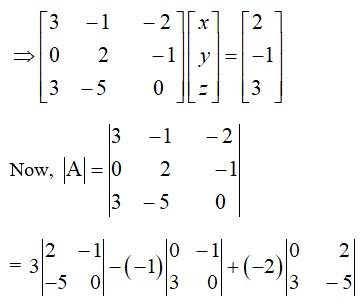
= -15 + 3 + 12
= -15 + 15
= 0
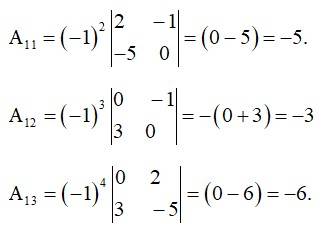
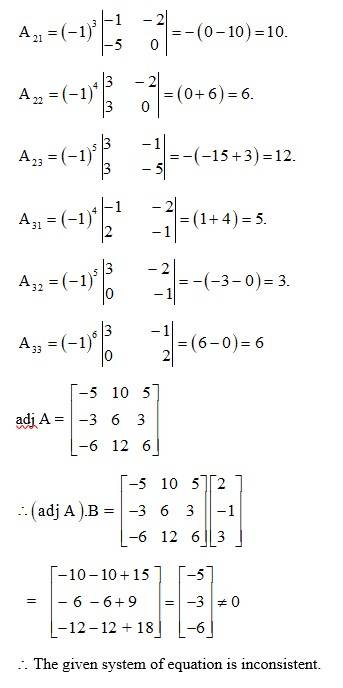
New answer posted
7 months agoContributor-Level 10
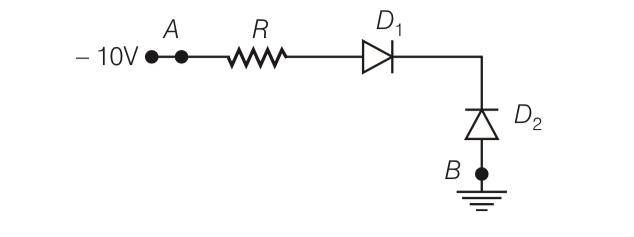
This is a Multiple Choice Questions as classified in NCERT Exemplar
Answer-b
Explanation- from the figure we can say that diode D1 is reverse biased and diode D2 is forward biased so current will flow from B to A.
New answer posted
7 months agoContributor-Level 10
The given system of eqn using matrix method can be expressed as
AK = B
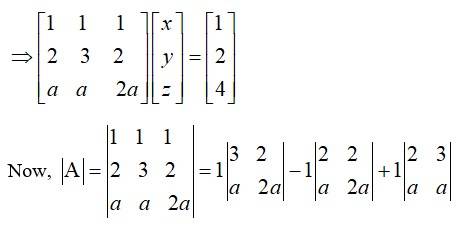
= 4a – 2a – a
= a ≠ 0.
Hence, the given system of eqn is consistent
New answer posted
7 months agoContributor-Level 10
This is a Multiple Choice Questions as classified in NCERT Exemplar
Explanation - When p-n junction is forward biased, it opposes the potential barrier junction, when p-n junction is reverse biased, it supports the potential barrier junction, resulting increase in potential barrier across the junction.
New answer posted
7 months agoContributor-Level 10
The given system of equation can be written in the form AK = B
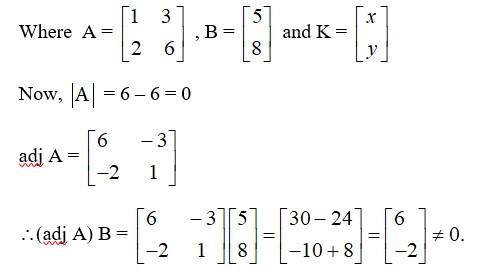
Hence the given system of eqn are inconsistent.
New answer posted
7 months agoContributor-Level 10
The given system of eqn can be written in the form AK = B where
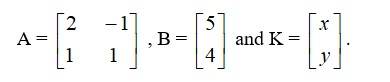
Now, = 2 – (-1) = 2 + 1 = 3 ≠ 0.
∴ The system of eqnis consistent.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 684k Reviews
- 1800k Answers