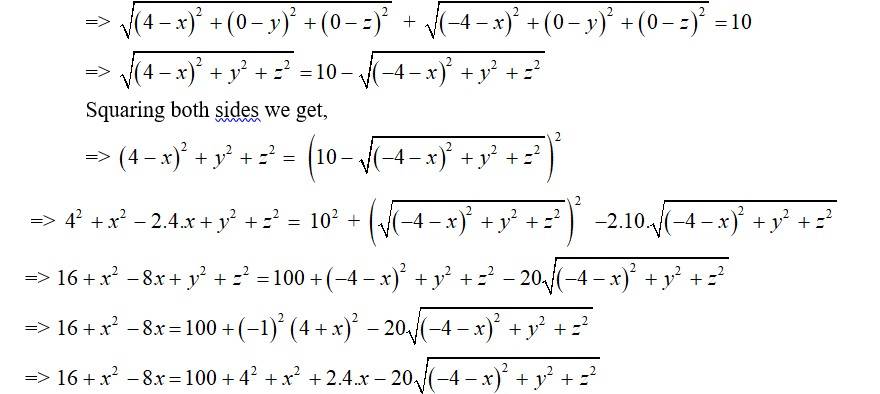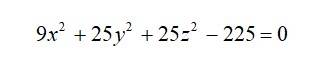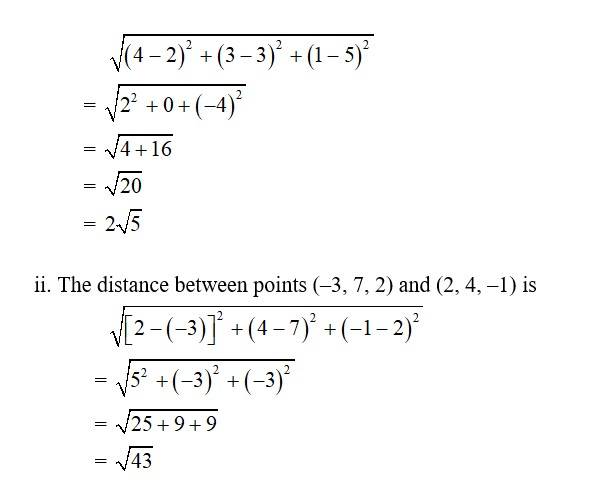Introduction to Three Dimensional Geometry

14. Let A(x₁, y₁, z₁) and B(x₂, y₂, z₂) trisect the line segment joining the points P(4, 2, –6) and Q(10, –16, 6).

Since A divides PQ internally in ratio 1 : 2. Then co-ordinates of A

= $\left(\frac{1(10)+2(4)}{1+2},\frac{1(-16)+2(2)}{1+2},\frac{1(6)+2(-6)}{1+2}\right)$

= $\left(\frac{10+8}{3},\frac{-16+4}{3},\frac{6-12}{3}\right)$

= $\left(\frac{18}{3},\frac{-12}{3},\frac{-6}{3}\right)$

= (6, –4, –2)

Similarly B divides PQ internally in ratio 2 : 1. Then co-ordinates of B

= $\left(\frac{2(10)+1(4)}{2+1},\frac{2(-16)+1(2)}{2+1},\frac{2(6)+1(-6)}{2+1}\right)$

= $\left(\frac{20+4}{3}·,·\frac{-32+2}{3}·,·\frac{12-6}{3}\right)$

= $\left(\frac{24}{3},\frac{-30}{3},\frac{6}{3}\right)$

= (8, –10, 2)

Hence the points which trisects the line segment joining the points P(4, 2, –6) and Q(10, –16, 6) are (6, –4, –2) and (8, –1)

13. Let P divides AB in ratio k : 1. Then co-ordinates of point P are

$(\frac{k(-1)+1(2)}{k+1},\frac{k(2)+1(-3)}{k+1},\frac{k(1)+1(4)}{k+1})$

= $\left(\frac{-k+2}{k+1},\frac{2k-3}{k+1},\frac{k+4}{k+1}\right)$

Let us examine whether the value of k, the point P coincides with point C

Putting $\frac{-k+2}{k + 1}=0$

=> $-k+2=0$

=> $k=2$

Put $k=2$ in

$\frac{2k - 3}{k + 1}$

= $\frac{2\left(2\right) - 3}{2 + 1}$

= $\frac{4 - 3}{3}$

= $\frac{1}{3}$

And put $k=2$ in

$\frac{k + 4}{k + 1}$

= $\frac{2 + 4}{2 + 1}$

= $\frac{6}{3}$

= 2

Therefore, C $\left(0,\frac{1}{3},2\right)$ is a point which divides AB internally in ratio 2 : 1 and is same as P. Hence A, B and C are collinear.

12. Let YZ-plane divides the line segment joining A (–2, 4, 7) and B (3, –5, 8) at point P (x, y, z) in the ratio k : 1.

Then the co-ordinates of P are.

$\left(\frac{k(3)+1(-2)}{k+1},\frac{k(-5)+1(4)}{k+1},\frac{k(8)+1(7)}{k+1}\right)$

$\left(\frac{3k-2}{k+1},\frac{-5k+4}{k+1},\frac{8k+7}{k+1}\right)$

As P lies on YZ-plane its x-coordinate is zero.

i.e. $\frac{3k-2}{k + 1}=0$

=> $3k-2=0$

=> $k=\frac{2}{3}$

Hence the YZ-plane divides AB internally in ratio.

$\frac{2}{3}$ : 1 = 2 : 3

11. Let point Q divides PR in the k : 1. Then co-ordinate of Q will be

$(\frac{k(9)+1(3)}{k+1},\frac{k(8)+1(2)}{k+1},\frac{k(-10)+1(-4)}{k+1})$

=> (5, 4, –6) = $·\left(\frac{9k+3}{k+1}·,·\frac{8k+2}{k+1}·,·\frac{-10k-4}{k+1}·\right)$

Equating the co-ordinates we get,

$\frac{9k+3}{k + 1}$ = 5

=> $9k+3=5\left(k+1\right)$

=> $9k+3=5k+5$

=> $9k-5k=5-3$

=> $4k=2$

=> $k=\frac{2}{4}$

=> $k=\frac{1}{2}$

Putting $k=\frac{1}{2}$ in y-coordinate and z-coordinate

$\frac{8k + 2}{k + 1}$

= $\frac{\left(8 x\frac{1}{2}\right) + 2}{\frac{1}{2} + 1}$

= (4 + 2) ÷ $\frac{3}{2}$

= 6 x $\frac{2}{3}$

= 4

And

$\frac{\left(-1\mathrm{0x}\frac{1}{2} \right) - 4}{\frac{1}{2} + 1}$

= (–5 – 4) ÷ $\frac{3}{2}$

= – 9 x $\frac{2}{3}$

= – 6

Which is matching with the given co-ordinates of Q.

Hence, the ration in which Q divides PR is k : 1

= $\frac{1}{2}$ : 1

= 1 : 2

10. i. Let P(x, y, z) be the point which divides line segment joining (–2, 3, 5) and (1, –4, 6) internally in the ratio 2 : 3

Therefore,

x = $\frac{2\left(1\right) + 3\left(-2\right)}{2 + 3}$ = $\frac{2 - 6}{5}$ = $\frac{-4}{5}$

y = $\frac{2\left(-4\right) + 3\left(3\right)}{2 + 3}$ = $\frac{-8 + 9}{5}$ = $\frac{1}{5}$

z = $\frac{2\left(6\right) + 3\left(5\right)}{2 + 3}$ = $\frac{12 + 15}{5}$ = $\frac{27}{5}$

Thus, the required points are $\left(\frac{-4}{5},\frac{1}{5},\frac{27}{5}\right)$

ii. Let P(x, y, z) be the point which divides line segment joining (–2, 3, 5) and (1, –4, 6) externally in the ratio 2 : 3

Therefore,

x = $\frac{2\left(1\right) - 3\left(-2\right)}{2 - 3}$ = $\frac{2 + 6}{-1}$ = –8

y = $\frac{2\left(-4\right) - 3\left(3\right)}{2 - 3}$ = $\frac{-8 - 9}{-1}$ = 17

z = $\frac{2\left(6\right) - 3\left(5\right)}{2 - 3}$ = $\frac{12 - 15}{-1}$ = 3

Thus, the required points are (–8, 17, 3).

9. Let P have the co-ordinates (x, y, z).

Given that,

PA + PB = 10

8. Let P(x, y, z) be the point equidistant from the given points (1, 2, 3) say A and (3, 2, –1) say B.

So, PA = PB

=>  ${\left(1-x\right)}^2+{\left(2-y\right)}^2+{\left(3-z\right)}^2$ = ${\left(3-x\right)}^2+{\left(2-y\right)}^2+{\left(-1-z\right)}^2$

Squaring both sides,

=> ${\left(1-x\right)}^2+{\left(2-y\right)}^2+{\left(3-z\right)}^2$ = ${\left(3-x\right)}^2+{\left(2-y\right)}^2+{\left(-1-z\right)}^2$

=> ${\left(1-x\right)}^2+{\left(3-z\right)}^2={\left(3-x\right)}^2+[{\left(-\right)}^2{\left(1+z\right)}^2$

=> $\left(1^2+x^2-2x\right)+\left(3^2+z^2-2.3.z\right)=\left(3^2+x^2-2.3.x\right)+(1^2+z^2+2z)$

=> $1+x^2-2x+9+z^2-6z=9+x^2-6x+1+z^2+2z$

=> $6x-2x-6z-2z=0$

=> $4x-8z=0$

=> $x-2z=0$

Therefore, the required equation of point is $x-2z=0$

5. i. The distance between points (2, 3, 5) and (4, 3, 1) is

4. i. The x-axis and y-axis taken together determine a plane known as XY plane.

ii. The coordinates of points in the XY-plane are of the form (x, y, 0).

iii. Coordinate planes divide the space into 8 (eight) octants.