Introduction to Three Dimensional Geometry
Get insights from 93 questions on Introduction to Three Dimensional Geometry, answered by students, alumni, and experts. You may also ask and answer any question you like about Introduction to Three Dimensional Geometry
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
4 months agoContributor-Level 10
This is a short answer type question as classified in NCERT Exemplar
New answer posted
4 months agoContributor-Level 10
This is a short answer type question as classified in NCERT Exemplar
New answer posted
4 months agoContributor-Level 10
This is a short answer type question as classified in NCERT Exemplar
New answer posted
4 months agoContributor-Level 10
7. i. Let the points be P (0, 7, –10), Q (1, 6, –6) and R (4, 9, –6)
So,
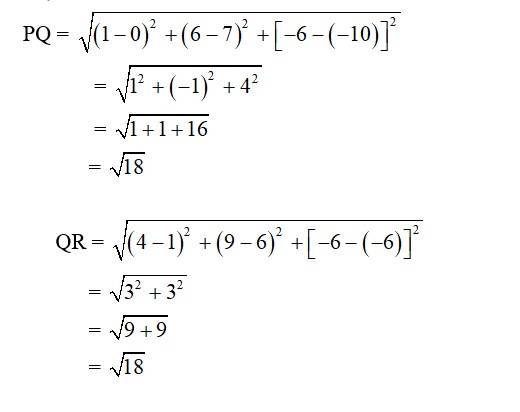




New answer posted
6 months agoContributor-Level 10
20. Let P have the coordinates (x, y, z)
Then,

=
=
=
=
And,
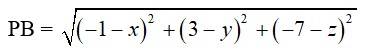
=> =
=
=
=
=
The equation of P such that,
=> +
=>
=>
=> =
New answer posted
6 months agoContributor-Level 10
19. Given, x-coordinate of R = 4
Let R divides line segment joining points P(2, –3, 4) and Q(8, 0,10) internally in the ratio k : 1. Then coordinate of R is
=
Then,
= 4
=>
=>
=>
=>
=>
=>
Hence,
=
=
=
=
And,
z =
=
=
=
= 6
Therefore, coordinates of R is (4, –2, 6).
New answer posted
6 months agoContributor-Level 10
18. Let Q be the point on y-axis which are at a distance from point P. As Q is on y-axis it has the coordinates of form (0, y, 0).
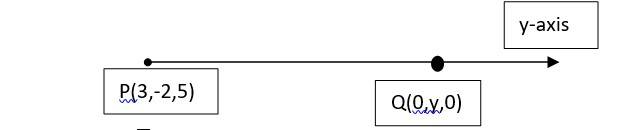
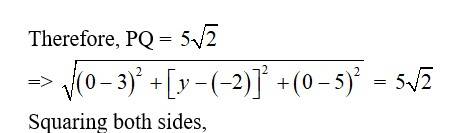
=>
=>
=>
=>
=>
So the coordinates Q are (0, 2, 0) and (0, –6, 0).
New answer posted
6 months agoContributor-Level 10
17. We know that, the centroid of a triangle with vertices (x1, y1, z1), (x2, y2, z2) and (x3, y3, z3) is
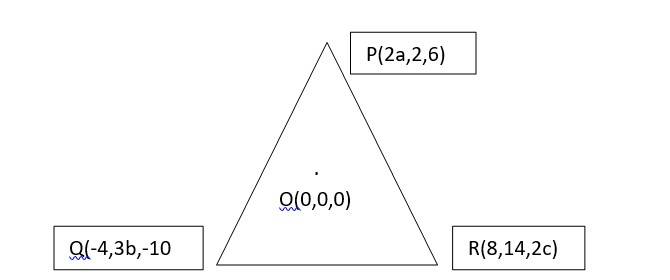
Equating the coordinates we get,
= 0
=>
=>
=>
=>
=>
And,
=>
=>
=>
=>
And,
=>
=>
=>
=>
=>
New answer posted
6 months agoContributor-Level 10
16. In a triangle ABC, the medians are the line segment that joins a vertex to the mid-point of the side that is opposite to that vertex. So, AE, BF and CG are the three medians.
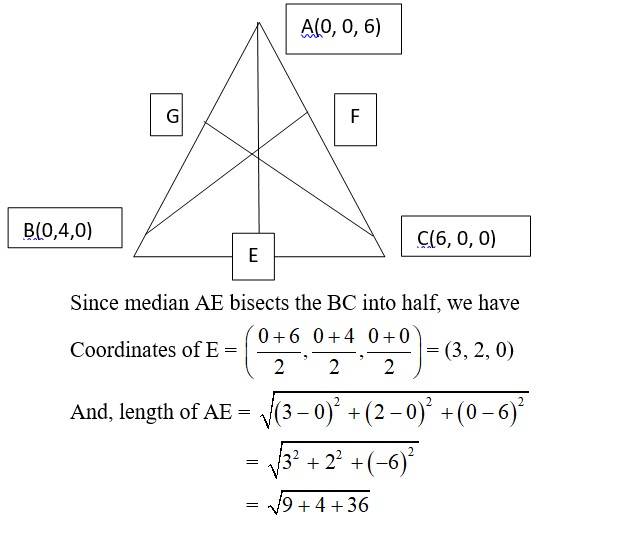

New answer posted
6 months agoContributor-Level 10
15. Let D(x, y, z) be the fourth vertex of the parallelogram ABCD.
In a parallelogram, the diagonal AC and BD bisects each other at point say O.
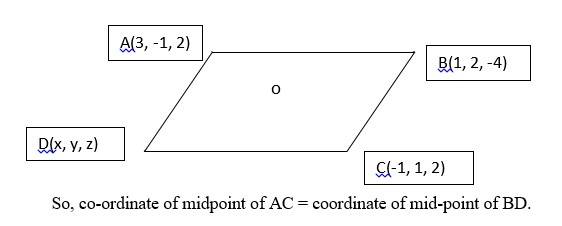
=>
=> (1, 0, 2) =
Equating the coordinates we get,
= 1
=>
=>
And
= 0
=>
And
= 2
=>
=>
=>
So, coordinates of fourth vertex is (1, –2, 8)
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 679k Reviews
- 1800k Answers
