Maths NCERT Exemplar Solutions Class 11th Chapter Eleven

${\displaystyle \underset{-a}{\overset{a}{\int }}\left(\left|x\right|+\left|x-2\right|\right)dx=22,a>2}$

${\displaystyle \underset{-a}{\overset{0}{\int }}\left(-2x+2\right)dx+{\displaystyle \underset{0}{\overset{2}{\int }}\left(x-x+2\right)dx+{\displaystyle \underset{2}{\overset{a}{\int }}\left(2x-2\right)dx=22}}}$

$\Rightarrow 2a^2+2=20\Rightarrow a^2=9\Rightarrow a=3$

$\therefore {\displaystyle \underset{3}{\overset{-3}{\int }}\left(x+\left[x\right]\right)dx=-{\displaystyle \underset{-3}{\overset{3}{\int }}\left(2x-\left\{x\right\}\right)dx=}}-{\displaystyle \underset{-3}{\overset{3}{\int }}2xdx+6}{{\displaystyle \underset{0}{\overset{1}{\int }}xdx=6.\frac{x^2}{2}}|}_0^1=3$           

$P=\left[\begin{array}{ccc}\hfill 3\hfill & \hfill -1\hfill & \hfill -2\hfill \\ \hfill 2\hfill & \hfill 0\hfill & \hfill \alpha \hfill \\ \hfill 3\hfill & \hfill -5\hfill & \hfill 0\hfill \end{array}\right]andQ=\left[q_{ij}\right]\Rightarrow PQ=k{l}_3$           

$q_{23}=-\frac{k}{8}and\left|Q\right|=\frac{k^2}{2}$            

$PQ=k{l}_3\Rightarrow P^{-1}=\frac{Q}{k}={\left(\begin{array}{ccc}\hfill 3\hfill & \hfill -1\hfill & \hfill -2\hfill \\ \hfill 2\hfill & \hfill 0\hfill & \hfill \alpha \hfill \\ \hfill 3\hfill & \hfill -5\hfill & \hfill 0\hfill \end{array}\right)}^{-1}$           

$\left|p\right|\left|Q\right|=\left(k{l}_3\right)\Rightarrow 8.\frac{k^2}{2}=k^3$

$k\ne 0\Rightarrow k=4$

$\therefore {\alpha }^2+k^2=1+16=17.$          

  $\overrightarrow{c}=\alpha \overrightarrow{a}+\beta \overrightarrow{b}.....\left(i\right)$

  $\overrightarrow{a}.\overrightarrow{c}=7\overrightarrow{b}.\overrightarrow{c}=0$         

$\overrightarrow{a}=-\widehat{i}+\widehat{j}+\widehat{k}\Rightarrow \left|\overrightarrow{a}\right|=\sqrt[]{3}$           

$\overrightarrow{b}=2\widehat{i}+\widehat{k}\Rightarrow \left|\overrightarrow{b}\right|=\sqrt[]{5}\overrightarrow{a}.\overrightarrow{b}=-2+1=-1$           

From   $\left(i\right)\overrightarrow{a}.\overrightarrow{c}=\alpha {\left|\overrightarrow{a}\right|}^2-\beta$

$3\alpha -\beta =7..........\left(ii\right)$           

$\overline{b}.\overline{c}=\alpha \overline{b}.\overline{a}+\beta {\left|\overrightarrow{b}\right|}^2\Rightarrow -\alpha +5\beta =0.......\left(iii\right)$           

Solving $\alpha =\frac{5}{2}and\beta =\frac{1}{2}$

$\Rightarrow 2{\left|\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\right|}^2=75$            

Let P (B₁) = a      P (B₂) = b            P (B₃) = c

Given a (1 – b) (1 – c) = a . (i)

b (1 – a) (1 – c) = b              . (ii)

c (1 – b) (1 – a) =  $\gamma$             . (iii)

(1 – a) (1 – b) (1 – c) = p     . (iv)

$\left(\alpha -2\beta \right)p=\alpha \beta$  

->a – ab – 2b + 2ab = ab Þ a = 2b . (v)

Again $\left(\beta -3\gamma \right)p=2\beta \gamma$  

-> b – bc – 3c + 3bc = 2bc Þ b = 3c   . (vi)

$\Rightarrow \frac{P\left(B_1\right)}{P\left(B_3\right)}=\frac{a}{c}=\frac{2b}{b/3}=6$        

  $x^2+y^2-2x-6y+6=0$ centre (1, 3)

$\begin{array}{l}r=\sqrt[]{1+9-6}=2\\ CM=\sqrt[]{1+4}=\sqrt[]{5}\end{array}$           

$r=\sqrt[]{5+4}=3$

Sum of elements $A\cap \left(B\cup C\right)=274*400$  

In set B numbers of the form 9k + 2 are {101, 109, .992}

  $\therefore sum=\frac{100}{2}\left(101+992\right)=\frac{100*1093}{2}......\left(i\right)$         

Another possible number is 9k + 5 forms are {104, .995}

  $\therefore sum=\frac{100}{2}\left(104+995\right)=\frac{100}{2}*1099.........\left(ii\right)$

$\therefore Total=\frac{100}{2}*\left[1093+1099\right]=100*1096=274*4*100=274*400$           

$\therefore$ possible value of $\mathcal{l}$ = 5

  $\frac{4}{sinx}+\frac{1}{1-sinx}=a\forall x\in \left(0,\frac{\pi }{2}\right)$

Let sin x = t, t  $\in$ (0, 1)

$g\left(t\right)=\frac{4}{t}+\frac{1}{1-t}$         

$g\text{'}\left(t\right)=0\Rightarrow t=\frac{2}{3}$           

$g\text{'}\text{'}\left(\frac{2}{3}\right)>0$           

$\therefore g{\left(t\right)}_{minimum}=\frac{4}{2/3}+\frac{1}{1-2/3}=9$          

Minimum value of a for which solution exist = 9

  $M=\left[\begin{array}{ccc}\hfill a_1\hfill & \hfill a_2\hfill & \hfill a_3\hfill \\ \hfill b_1\hfill & \hfill b_2\hfill & \hfill c_3\hfill \\ \hfill c_1\hfill & \hfill c_2\hfill & \hfill c_3\hfill \end{array}\right]$

$M^{T}M=\left[\begin{array}{ccc}\hfill a_1\hfill & \hfill b_1\hfill & \hfill c_1\hfill \\ \hfill a_2\hfill & \hfill b_2\hfill & \hfill c_2\hfill \\ \hfill a_3\hfill & \hfill b_3\hfill & \hfill c_3\hfill \end{array}\right]\left[\begin{array}{ccc}\hfill a_1\hfill & \hfill a_2\hfill & \hfill a_3\hfill \\ \hfill b_1\hfill & \hfill b_2\hfill & \hfill b_3\hfill \\ \hfill c_1\hfill & \hfill c_2\hfill & \hfill c_3\hfill \end{array}\right]$     

$Tr\left(M^{T}M\right)=a_1^2+b_1^2+c_1^2+a_2^2+b_2^2+c_2^2+a_3^2+b_3^2+c_3^2=7$           

all  $a_i,b_i,c_i\in \left\{0,1,2\right\}for$  i = 1, 2, 3

Case 1 7 one's and two zeroes which can occur in 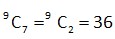ways

Case 2 One 2 three 1's five zeroes =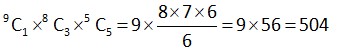

total such matrices = 504 + 36 = 540

$z+\alpha \left|z-1\right|+2i=0$

Let z = x + iy

$\Rightarrow x+i\left(y+2\right)=-\alpha \sqrt[]{{\left(x-1\right)}^2+y^2}$            

for $\alpha \in Ry+2=0\Rightarrow y=-2$

 $x^2={\alpha }^2\left[{\left(x-1\right)}^2+4\right]$

$x^2\left(\frac{1}{{\alpha }^2}-1\right)+2x-5$

$\frac{1}{{\alpha }^2}\ge \frac{4}{5}\Rightarrow {\alpha }^2\le \frac{5}{4}\Rightarrow \frac{-\sqrt[]{5}}{2}\le \alpha \le \frac{\sqrt[]{5}}{2}$

$4\left(p^2+q^2\right)=4\left(\frac{5}{4}+\frac{5}{4}\right)=10$          

= 0

${\displaystyle \sum _{r=1}^{n}ta{n}^{-1}\frac{1}{1+r+r^2}={\displaystyle \sum _{r=1}^{n}ta{n}^{-1}\frac{\left(r+1\right)}{1+r\left(r+1\right)}}}$  

$=ta{n}^{-1}2-ta{n}^{-1}+......+ta{n}^{-1}\left(n+1\right)-ta{n}^{-1}n$            

For n  $\infty$ ->value = $\frac{\pi }{2}-\frac{\pi }{4}=\frac{\pi }{4}$  

$\therefore tan\left(\frac{\pi }{4}\right)=1$