- Conic Section Short Answer Type Questions
- Conic Section Long Answer Type Questions
- Conic Section True or False Type Questions
- Conic Section Fill in the Blanks Type Questions
- Conic Section Objective Type Questions
- JEE_Mains_01 MT
Conic Section Short Answer Type Questions
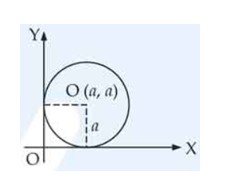
| 1. Find the equation of the circle which touches both axes in the first quadrant and whose radius is . |
| Sol. |
| 2. Show that the point given by and lies on a circle for all real values of , such that , where is any given real number. |
| Sol. |
Commonly asked questions
Find the equation of the circle which touches both axes in the first quadrant and whose radius is .
This is a short answer type question as classified in NCERT Exemplar
Show that the point given by and lies on a circle for all real values of , such that , where is any given real number.
This is a short answer type question as classified in NCERT Exemplar
If a circle passes through the points , then find the coordinates of its center.
This is a short answer type question as classified in NCERT Exemplar
Find the equation of the circle which touches the -axis and whose center is .
This is a short answer type question as classified in NCERT Exemplar
If the lines and are tangents to a circle, then find the radius of the circle.
[Hint: Distance between given parallel lines gives the diameter of the circle.]
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
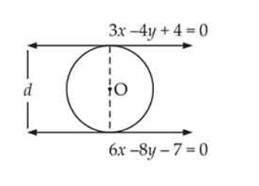
Sol:
Find the equation of a circle which touches both axes and the line and lies in the third quadrant.
[Hint: Let be the radius of the circle, then will be the center, and the perpendicular distance from the center to the given line gives the radius of the circle.]
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
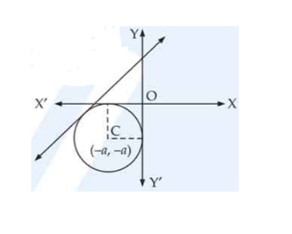
Sol:
If one end of a diameter of the circle is , then find the coordinates of the other end of the diameter.
This is a Short Answer Type Questions as classified in NCERT Exemplar
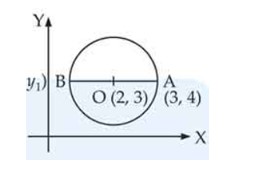
Sol:
Find the equation of the circle having as its center and passing through the line , .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If the line touches the circle , then find the value of .
[Hint: Equate perpendicular distance from the center of the circle to its radius.]
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the equation of a circle concentric with the circle and has double its area.
[Hint: Concentric circles have the same center.]
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If the latus rectum of an ellipse is equal to half of its minor axis, then find its eccentricity.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Sol:
Given the ellipse with equation , find the eccentricity and foci.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If the eccentricity of an ellipse is and the distance between its foci is 10, then find the latus rectum of the ellipse.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the equation of the ellipse whose eccentricity is , latus rectum is 5, and the center is (0, 0)
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the distance between the directrices of the ellipse .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
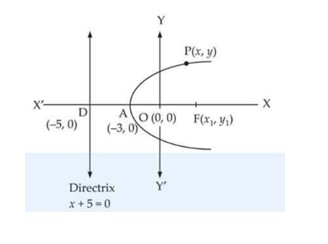
Find the coordinates of a point on the parabola whose focal distance is 4.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
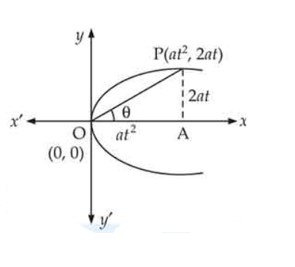
Find the length of the line segment joining the vertex of the parabola and a point on the parabola where the line segment makes an angle to the x-axis.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If the points (0, 4) and (0, 2) are respectively the vertex and focus of a parabola, then find the equation of the parabola.
This is a Short Answer Type Questions as classified in NCERT Exemplar
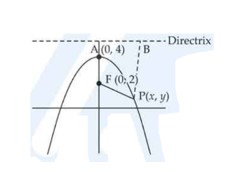
Sol:
If the line is tangent to the parabola , then find the value of .
[Hint: Solving the equation of the line and parabola, obtain a quadratic equation and apply the tangency condition to find ].
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If the distance between the foci of a hyperbola is 16 and its eccentricity is, then obtain the equation of the hyperbola.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the eccentricity of the hyperbola .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the equation of the hyperbola with eccentricity and foci at .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Conic Section Long Answer Type Questions
| 1. If the lines and are the diameters of a circle with an area of 154 square units, then obtain the equation of the circle. |
| Sol:
|
| 2. Find the equation of the circle which passes through the points (2, 3) and (4, 5), and its center lies on the straight line . |
| Sol:
|
Commonly asked questions
If the lines and are the diameters of a circle with an area of 154 square units, then obtain the equation of the circle.
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the equation of the circle which passes through the points (2, 3) and (4, 5), and its center lies on the straight line .
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
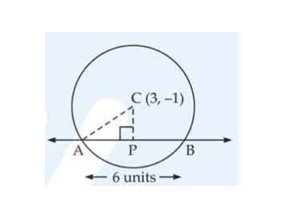
Find the equation of a circle whose center is (3, -1) and which cuts off a chord of length 6 units on the line .
[Hint: To determine the radius of the circle, find the perpendicular distance from the center to the given line.]
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
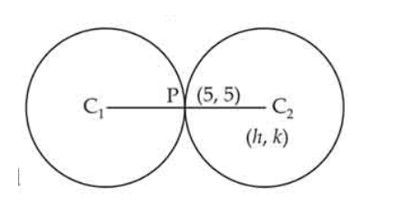
Find the equation of a circle of radius 5 which is touching another circle at (5, 5).
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the equation of a circle passing through the point (7, 3), having a radius of 3 units, and whose center lies on the line .
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the equation of each of the following parabolas:
Directrix , focus at (6, 0).
Vertex at (0, 4), focus at (0, 2).
Focus at (-1,-2), directrix .
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
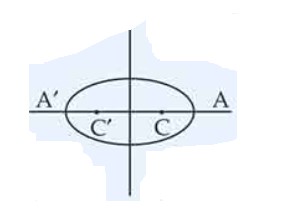
Find the equation of the set of all points the sum of whose distances from the points (3, 0) and (9, 0) is 12.
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
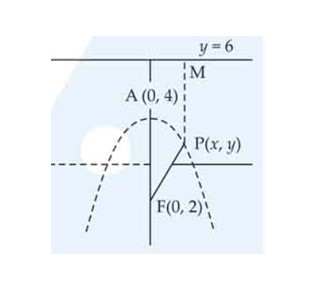
Find the equation of the set of all points whose distance from (0, 4) equals their distance from the line
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Show that the set of all points such that the difference of their distances from (4, 0) and (-4, 0) is always equal to 2 represents a hyperbola.
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the equation of the hyperbola with:
Vertices , foci .
Vertices , eccentricity .
Foci , passing through (2, 3).
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Conic Section True or False Type Questions
| 1. The line is a diameter of the circle . True or False? |
| Sol:
|
| 2. The shortest distance from the point (2, -7) to the circle is equal to 5. [Hint: The shortest distance is equal to the difference of the radius and the distance between the center and the given point.] |
| Sol:
|
Commonly asked questions
The line is a diameter of the circle . True or False?
This is a true and false Type Questions as classified in NCERT Exemplar
Sol:
The shortest distance from the point (2, -7) to the circle is equal to 5.
[Hint: The shortest distance is equal to the difference of the radius and the distance between the center and the given point.]
This is a true and false Type Questions as classified in NCERT Exemplar
Sol:
If the line is a tangent to the circle , then the point (l, m) lies on a circle. True or False?
This is a true and false Type Questions as classified in NCERT Exemplar
Sol:
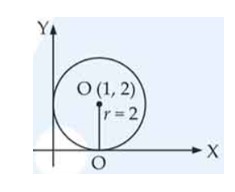
The point (1, 2) lies inside the circle . True or False?
This is a True and False Type Questions as classified in NCERT Exemplar
Sol:
The line will touch the parabola if . True or False?
This is a True and False Type Questions as classified in NCERT Exemplar
Sol:
If is a point on the ellipse , whose foci are and , then
This is a True and False Type Questions as classified in NCERT Exemplar
Sol:
The line touches the ellipse at the point (3, 2). True or False?
This is a True and False Type Questions as classified in NCERT Exemplar
Sol:
The locus of the point of intersection of lines and for different values of is a hyperbola whose eccentricity is 2.
[Hint: Eliminate between the given equations.]
This is a True and False Type Questions as classified in NCERT Exemplar
Sol:
Conic Section Fill in the Blanks Type Questions
| 1. The equation of the circle having its center at (3,-4) and touching the line is ______. [Hint: To determine the radius, find the perpendicular distance from the center of the circle to the line.] |
| Sol:
|
| 2. The equation of the circle circumscribing the triangle whose sides are the lines , , and is ______. |
| Sol:
|
Commonly asked questions
The equation of the circle having its center at (3,-4) and touching the line is ______.
[Hint: To determine the radius, find the perpendicular distance from the center of the circle to the line.]
This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar
Sol:
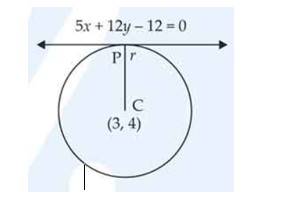
The equation of the circle circumscribing the triangle whose sides are the lines , , and is ______.
This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar
Sol:
An ellipse is described by using an endless string that passes over two pins. If the axes are 6 cm and 4 cm, the length of the string and the distance between the pins are ______.
This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar
Sol:
The equation of the ellipse having foci (0, 1), (0, –1), and a minor axis of length 1 is ______.
This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar
Sol:
The equation of the parabola having focus at (–1, –2) and the directrix is ______.
This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar
Sol:
The equation of the hyperbola with vertices at , eccentricity , and foci at is ______
This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar
Sol:
Conic Section Objective Type Questions
| 1. The area of the circle centered at (1, 2) and passing through (4, 6) is (a) (b) (c) (d) None of these |
| Sol:
|
| 2. The equation of a circle that passes through (3, 6) and touches the axes is (a)
|
| Sol:
|
Commonly asked questions
The area of the circle centered at (1, 2) and passing through (4, 6) is
(a)
(b)
(c)
(d) None of these
This is an objective Type Questions as classified in NCERT Exemplar
Sol:
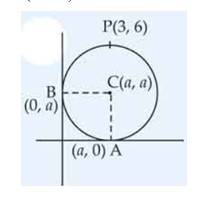
The equation of a circle that passes through (3, 6) and touches the axes is
(a)
(b)
(c)
(d) None of these
This is an objective Type Questions as classified in NCERT Exemplar
Sol:
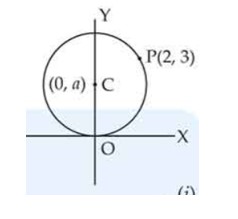
The equation of the circle with its center on the y-axis and passing through the origin and the point (2, 3) is
(a)
(b)
(c)
(d) None of these
This is an objective Type Questions as classified in NCERT Exemplar
Sol:
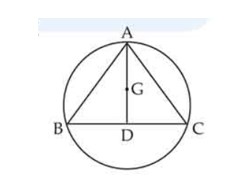
The equation of a circle with the origin as the center and passing through the vertices of an equilateral triangle whose median is of length is
(a)
(b)
(c)
(d)
[Hint: The centroid of the triangle coincides with the center of the circle, and the radius is of the median.]
This is an objective Type Questions as classified in NCERT Exemplar
Sol:
If the focus of a parabola is (0, -3) and its directrix is , then its equation is
(a)
(b)
(c)
(d)
This is an objective Type Questions as classified in NCERT Exemplar
Sol:
If the parabola passes through the point (3, 2), then the length of its latus rectum is
(a)
(b) 2
(c) 4
(d) None of these
This is an objective Type Questions as classified in NCERT Exemplar
Sol:
If the vertex of the parabola is at the point (–3, 0) and the directrix is the line , then its equation is
(a)
(b)
(c)
(d)
This is an objective Type Questions as classified in NCERT Exemplar
Sol:
The equation of the ellipse whose focus is (1, –1), the directrix is the line , and the eccentricity is is
(a)
(b)
(c)
(d) None of these
This is an objective Type Questions as classified in NCERT Exemplar
Sol:
The length of the latus rectum of the ellipse is
(a) 4
(b) 3
(c)
(d)
This is an objective Type Questions as classified in NCERT Exemplar
Sol:
If is the eccentricity of the ellipse (where ), then
(a)
(b)
(c)
(d)
This is an objective Type Questions as classified in NCERT Exemplar
Sol:
The eccentricity of the hyperbola whose latus rectum is 8 and conjugate axis is half the distance between the foci is
(a)
(b)
(c)
(d) None of these
This is an objective Type Questions as classified in NCERT Exemplar
Sol:
The distance between the foci of a hyperbola is 16, and its eccentricity is 2. Its equation is
(a)
(b)
(c)
(d) None of these
This is an objective Type Questions as classified in NCERT Exemplar
Sol:
The equation of the hyperbola with eccentricity and foci at is
(a)
(b)
(c)
(d) None of these
This is an objective Type Questions as classified in NCERT Exemplar
Sol:
JEE_Mains_01 MT
JEE_Mains_01 MT
Maths NCERT Exemplar Solutions Class 11th Chapter Eleven Exam