Maths
Get insights from 6.5k questions on Maths, answered by students, alumni, and experts. You may also ask and answer any question you like about Maths
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
3 months agoContributor-Level 10
a = i + j + 2k
b = -i + 2j + 3k
a + b = 3j + 5k
a . b = -1 + 2 + 6 = 7
a * b = |i, j, k; 1, 2; -1, 2, 3| = -i - 5j + 3k
(a - b) * b) = (a * b) - (b * b) = a * b
(a * (a - b) * b) = a * (a * b) = (a . b)a - (a . a)b = 7a - 6b
. The expression becomes (a + b) * (7a - 6b) * b)
= (a + b) * (7 (a * b)
= 7 [ (a * (a * b) + (b * (a * b) ]
= 7 [ (
New answer posted
3 months agoContributor-Level 10
sinθ + cosθ = 1/2
16 (sin (2θ) + cos (4θ) + sin (6θ)
= 16 [2sin (4θ)cos (2θ) + cos (4θ)]
= 16 [4sin (2θ)cos² (2θ) + 2cos² (2θ) - 1] . (i)
Now, sinθ + cosθ = 1/2, squaring on both sides, we get
1 + sin (2θ) = 1/4
sin (2θ) = -3/4
cos² (2θ) = 1 - sin² (2θ) = 1 - 9/16 = 7/16
From equation (i)
16 [4 (-3/4) (7/16) + 2 (7/16) - 1]
16 [-21/16 + 14/16 - 16/16] = 16 [-23/16] = -23
New answer posted
3 months agoContributor-Level 10
S? : |z - 3 - 2i|² = 8
|z - (3 + 2i)| = 2√2
(x - 3)² + (y - 2)² = (2√2)²
S? : Re (z) ≥ 5
x ≥ 5
S? : |z - z? | ≥ 8
|2iy| ≥ 8
2|y| ≥ 8
|y| ≥ 4
y ≥ 4 or y ≤ -4
From the graph of the circle (S? ) and the regions (S? and S? ), we can see that there is one point of intersection at (5, 4).
∴ n (S? ∩ S? ∩ S? ) = 1
New answer posted
3 months agoContributor-Level 10
x² - |x| - 12 = 0
Case 1: x ≥ 0, |x| = x
x² - x - 12 = 0
(x-4) (x+3) = 0, x=4 (x=-3 is rejected)
Case 2: x < 0, |x| = -x
x² + x - 12 = 0
(x+4) (x-3) = 0, x=-4 (x=3 is rejected)
Two real solutions: 4 and -4.
New answer posted
3 months agoContributor-Level 10
x² - 4xy – 5y² = 0
Equation of pair of straight line bisectors is (x²-y²)/ (a-b) = xy/h
(x²-y²)/ (1- (-5) = xy/ (-2)
(x²-y²)/6 = xy/ (-2)
x²-y² = -3xy
x² + 3xy - y² = 0
New answer posted
3 months agoContributor-Level 10
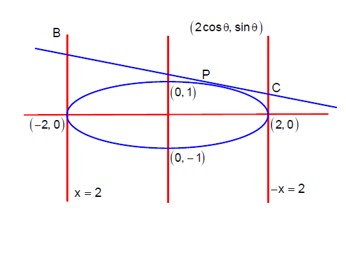
Equation of tangent of P (2cosθ, sinθ) is
(cosθ)x + (2sinθ)y = 4
Solving equation of tangent with equation of tangents at major axis ends, i.e. x = -2 and x = 2
For point 'B' (at x=-2):
-2cosθ + 2sinθ y = 4 ⇒ y = (2+cosθ)/sinθ
B (-2, (2+cosθ)/sinθ)
For point 'C' (at x=2):
2cosθ + 2sinθ y = 4 ⇒ y = (2-cosθ)/sinθ
C (2, (2-cosθ)/sinθ)
Now BC is the diameter of circle
Equation of circle: (x+2) (x-2) + (y - (2+cosθ)/sinθ) (y - (2-cosθ)/sinθ) = 0
x²-4 + y² - (4/sinθ)y + (4-cos²θ)/sin²θ = 0
Check if (√3, 0) satisfies this:
(√3)²-4 + 0 - 0 + (4-cos²θ)/sin²θ = -1 + (3+sin²θ)/sin²θ = -1 + 3/sin²θ + 1 = 3/sin²
New answer posted
3 months agoContributor-Level 10
ai+aj+ck, i+k and ci+cj+bk are co-planar,
|a c; 1 0 1; c b| = 0
a (0-c) - a (b-c) + c (c-0) = 0
-ac - ab + AC + c² = 0
c² = ab
c = √ab
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 679k Reviews
- 1800k Answers