Tags Maths

Maths

Get insights from 6.5k questions on Maths, answered by students, alumni, and experts. You may also ask and answer any question you like about Maths

Follow Ask Question

6.5k

Questions

Discussions

Active Users

Followers

New answer posted

6 months ago

Maths Differential Equations

65. Kindly Consider the following

0 Follower 2 Views

Vishal Baghel

Contributor-Level 10

Kindly go through the solution

Integrating both sides,

0 0

New answer posted

6 months ago

Maths Continuity and Differentiability

114. If f:[-5,5] →R is a differentiable function and if f'(x) does not vanish anywhere, then prove that f(-5) ≠ f(5).

0 Follower 2 Views

alok kumar singh

Contributor-Level 10

114. Solution :
It is given that f: [-5,5]? R is a differentiable function.

Since every differentiable function is a continuous function, we obtain

(a) f is continuous on [?5, 5].

(b) f is differentiable on (?5, 5).

Therefore, by the Mean Value Theorem, there exists c? (?5, 5) such that

$\begin{array}{l} f^{'} (c) \frac{f (5) ? f (? 5)}{5 ? (? 5)} \\ ? 10 f^{'} (c) = f (5) ? f (? 5) \end{array}$

It is also given that f' (x) does not vanish anywhere.

$\begin{array}{l} ? f^{'} (c) ? 0 \\ ? 10 f^{'} (c) ? 0 \\ ? f (5) ? f (? 5) ? 0 \\ ? f (5) ? f (? 5) \end{array}$

Hence, proved.

0 0

New answer posted

6 months ago

Maths Binomial Theorem

2. Prove that $\sum_{r = 0}^{n} 3^{r}^{n} C_{r} = 4^{n} .$

0 Follower 3 Views

Payal Gupta

Contributor-Level 10

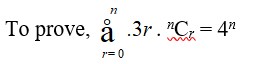
By binomial theorem,

(a + b)ⁿ = ⁿC₀ (a)ⁿ (b)⁰ + ⁿC₁ (a)ⁿ^–1 (b)¹ + …………. + ⁿC_r (a)ⁿ^–r (b)^r + …………… + ⁿC_n (a)ⁿ^–n (b)ⁿ

Where, b⁰ = 1 = aⁿ^–n

So, (a + b)ⁿ = ⁿC_r (a)ⁿ^–r (b)^r

Putting a = 1 and b = 3 such that a + b = 4, we can rewrite the above equation as

(1 + 3)ⁿ = ⁿC_r (1)ⁿ^–r.3^r

=>4ⁿ = $\underset{r = 0}{?} . 3 r$ .ⁿC_r

Hence proved.

0 0

New answer posted

6 months ago

Maths Differential Equations

64. $x^{2} \frac{d y}{d x} = x^{2} - 2 y^{2} + x y$

0 Follower 2 Views

Vishal Baghel

Contributor-Level 10

The given D.E. is

$\begin{array}{l} x^{2} \frac{d y}{d x} = x^{2} - 2 y^{2} + + x y \\ \Rightarrow \frac{d y}{d x} = \frac{x^{2} - 2 y^{2} + + x y}{x^{2}} = 1 - \frac{2 y^{2}}{x^{2}} + \frac{y}{x} \\ \Rightarrow \frac{d y}{d x} = 1 - 2 {(\frac{y}{x})}^{2} + \frac{y}{x} = f (\frac{y}{x}) \end{array}$

Hence, the D.E. is homogenous $f x^{n}$

Let, $y = v x . = \frac{y}{x} = v$ so that, $\frac{d y}{d x} = v + x \frac{d v}{d x}$ is the D.E.

Thus, $v + x \frac{d v}{d x} = 1 - 2 v^{2} + v$

$\begin{array}{l} \Rightarrow x \frac{d v}{d x} = 1 - 2 v^{2} \\ \Rightarrow \frac{d v}{1 - 2 v^{2}} = \frac{d x}{x} \end{array}$

Integrating both sides,

0 0

New answer posted

6 months ago

Maths Differential Equations

63. $(x^{2} - y^{2}) d x + 2 x y d y = 0$

0 Follower 2 Views

Vishal Baghel

Contributor-Level 10

The Given D.E. is

$\begin{array}{l} (x^{2} - y^{2}) d x + 2 x y d y = 0 \\ \Rightarrow 2 * y d y = - (x^{2} - y^{2}) d x \\ = \frac{d y}{d x} = - \frac{(x^{2} - y^{2})}{2 x y} = \frac{(y^{2} - x^{2})}{2 x y} \\ = \frac{1}{2} \frac{(\frac{y^{2} - x^{2}}{x^{2}})}{(\frac{x y}{x^{2}})} \\ = \frac{1}{2} \frac{[{(\frac{y}{x})}^{2} - 1]}{(\frac{y}{x})} = f (\frac{y}{x}) \end{array}$

Hence, the given D.E. is homogenous.

Let, $y = v x \Rightarrow \frac{y}{x} = v, s o t h a t, \frac{d y}{d x} = v + x \frac{d v}{d x}$ in the D.E

$\begin{array}{l} \Rightarrow v + x \frac{d v}{d x} = \frac{1}{2} [\frac{v^{2} - 1}{v}] \\ \Rightarrow x \frac{d v}{d x} = \frac{v^{2} - 1}{2 v} - v = \frac{v^{2} - 1 - 2 v^{2}}{2 v} = \frac{- 1 - v^{2}}{2 v} \\ \Rightarrow (\frac{2 v}{1 + v^{2}}) d v = - \frac{d x}{x} \end{array}$

Integrating both sides we get,

Putting back $v = \frac{y}{x}$ we get,

$\begin{array}{l} \Rightarrow x [\frac{y^{2}}{x^{2}} + 1] = c \\ \Rightarrow \frac{y^{2} + x^{2}}{x} = c \end{array}$

$\Rightarrow y^{2} + x^{2} = x c$ is the required solution.

0 0

New answer posted

6 months ago

Maths Differential Equations

62. $(x - y) d y - (x + y) d x = 0$

0 Follower 2 Views

Vishal Baghel

Contributor-Level 10

The Given D.E. is $(x - y) d y - (x + y) d x = 0$

$\begin{array}{l} \Rightarrow (x - y) d y = (x + y) d x \\ \Rightarrow \frac{d y}{d x} = \frac{x + y}{x - y} = \frac{x (1 + \frac{y}{x})}{x (1 - \frac{y}{x})} = \frac{1 + \frac{y}{x}}{1 - \frac{y}{x}} = f (\frac{y}{x}) \end{array}$

Hence, the given D.E. is homogenous.

Let, $y = v x = \frac{y}{x} = v, s o, \frac{d y}{d x} = v + x \frac{d v}{d x}$ in the D.E

Then, $\begin{array}{l} v + x \frac{d v}{d x} = \frac{1 + v}{1 - v} \\ \Rightarrow x \frac{d v}{d x} = \frac{1 + v}{1 - v} - v = \frac{1 + v - 1 + v^{2}}{1 - v} = \frac{1 + v^{2}}{1 - v} \\ \Rightarrow [\frac{1 - v}{1 + v^{2}}] d v = \frac{d x}{x} \end{array}$

Integrating both sides,

$\begin{array}{l} \int \frac{1 - v}{1 + v^{2}} d v = \int \frac{d x}{x} \\ \Rightarrow \int \frac{1}{1 + v^{2}} d v - \frac{1}{2} \int \frac{2 v}{1 + v^{2}} d v = l o g x + c \\ \Rightarrow t a n^{- 1} v - \frac{1}{2} l o g (1 + v^{2}) = l o g x + c \end{array}$

Putting back $v = \frac{y}{x}, w e g e t,$

$\begin{array}{l} = t a n^{- 1} \frac{y}{x} - \frac{1}{2} l o g | 1 + \frac{y^{2}}{x^{2}} | = l o g x + c \\ = t a n^{- 1} \frac{y}{x} - \frac{1}{2} l o g | \frac{x^{2} + y^{2}}{x^{2}} | = l o g x + c \\ = t a n^{- 1} \frac{y}{x} - \frac{1}{2} [l o g (x^{2} + y^{2}) - l o g x^{2}] = l o g x + c \end{array}$

$\begin{array}{l} = t a n^{- 1} \frac{y}{x} - \frac{1}{2} l o g (x^{2} + y^{2}) + \frac{1}{2} l o g x^{2} = l o g x + c \\ = t a n^{- 1} \frac{y}{x} - \frac{1}{2} l o g (x^{2} + y^{2}) + l o g {(x^{2})}^{\frac{1}{2}} = l o g x + c \\ = t a n^{- 1} \frac{y}{x} - \frac{1}{2} l o g (x^{2} + y^{2}) + l o g x = l o g + c \\ = t a n^{- 1} \frac{y}{x} = \frac{1}{2} l o g (x^{2} + y^{2}) + c \end{array}$

0 0

New answer posted

6 months ago

Maths Continuity and Differentiability

113. Examine if Rolle's Theorem is applicable to any of the following functions. Can you say something about the converse of Rolle's Theorem from these examples?

$f (x) = [x]$ for $x \in [5, 9]$

$f (x) = [x]$ for $x \in [- 2, 2]$

$f (x) = x^{2} - 1$ for $x \in [1, 2]$

0 Follower 2 Views

alok kumar singh

Contributor-Level 10

113. Solution:

By Rolle's Theorem, for a function $f [a, b] \to R,$ if

f is continuous on $[a, b]$

f is differentiable on $(a, b)$

f(a)= f(b)

then, there exists some $c \in (a, b)$ such that $f^{'} (c) = 0$

therefore, Rolle's Theorem is not applicable to those functions that do not satisfy any of the three conditions of the hypothesis.

$f (x) = [x]$ for $x \in [5, 9]$

It is evident that the given function f(x) is not continuous at every integral point.

In particular, f(x) is not continuous at x=5 and x=9

$\Rightarrow$ f(x) is not continuous in $[5, 9]$

Also, $\begin{array}{l} f (5) = [5] = 5, a n d, f (9) = [9] = 9 \\ ∴ f (5) \neq f (9) \end{array}$

The differentiability of f in $(5, 9)$ is checked as follows.

Let n be an integer such that $n \in (5, 9)$ .

The left hand limit of f at x

...more

113. Solution:

By Rolle's Theorem, for a function $f [a, b] \to R,$ if

f is continuous on $[a, b]$

f is differentiable on $(a, b)$

f(a)= f(b)

then, there exists some $c \in (a, b)$ such that $f^{'} (c) = 0$

therefore, Rolle's Theorem is not applicable to those functions that do not satisfy any of the three conditions of the hypothesis.

$f (x) = [x]$ for $x \in [5, 9]$

It is evident that the given function f(x) is not continuous at every integral point.

In particular, f(x) is not continuous at x=5 and x=9

$\Rightarrow$ f(x) is not continuous in $[5, 9]$

Also, $\begin{array}{l} f (5) = [5] = 5, a n d, f (9) = [9] = 9 \\ ∴ f (5) \neq f (9) \end{array}$

The differentiability of f in $(5, 9)$ is checked as follows.

Let n be an integer such that $n \in (5, 9)$ .

The left hand limit of f at x=n is,

$\underset{h \to 0}{l i m} \frac{f (n + h) - f (n)}{h} = \underset{h \to 0}{l i m} \frac{[n + h] - [n]}{h} = \underset{h \to 0}{l i m} \frac{n - 1 - n}{h} = \underset{h \to 0}{l i m} \frac{- 1}{h} = \infty$

The right hand limit of f at x=n is,

$\underset{h \to 0}{l i m} \frac{f (n + h) - f (n)}{h} = \underset{h \to 0}{l i m} \frac{[n + h] - [n]}{h} = \underset{h \to 0}{l i m} \frac{n - n}{h} = \underset{h \to 0}{l i m} 0 = 0$

Since the left and right hand limits of f at x=n are not equal, f is not differentiable at x=n

$∴$ f is not differentiable in (5,9).

It is observed that f does not satisfy all the conditions of the hypothesis of Rolle's Theorem.

Hence, Rolle's Theorem is not applicable for $f (x) = [x]$ for $x \in [5, 9]$

$f (x) = [x]$ for $x \in [- 2, 2]$

It is evident that the given function f(x) is not continuous at every integral point.

In particular, f(x) is not continuous at x=-2 and x=2

$\Rightarrow$ f(x) is not continuous in $[- 2, 2]$ .

Also, $\begin{array}{l} f (- 2) = [- 2] = - 2, a n d, f (2) = [2] = 2 \\ ∴ f (- 2) \neq f (2) \end{array}$

The differentiability of f in $(- 2, 2)$ is checked as follows.

Let n be an integer such that $n \in (- 2, 2)$ .

The left hand limit of f at x=n is,

The right hand limit of f at x=n is,

$\underset{h \to 0}{l i m} \frac{f (n + h) - f (n)}{h} = \underset{h \to 0}{l i m} \frac{[n + h] - [n]}{h} = \underset{h \to 0}{l i m} \frac{n - n}{h} = \underset{h \to 0}{l i m} 0 = 0$

Since the left- and right-hand limits of f at x=n are not equal, f is not differentiable at x=n

$∴$ f is not differentiable in (-2,2).

It is observed that f does not satisfy all the conditions of the hypothesis of Rolle's Theorem.

Hence, Rolle's Theorem is not applicable for $f (x) = [x]$ for $x \in [- 2, 2]$

$f (x) = x^{2} - 1$ for $x \in [1, 2]$

It is evident that f, being a polynomial function, is continuous in $[1, 2]$ and is differentiable on (1,2).

$\begin{array}{l} f (1) = 1^{2} = 0 \\ f (2) = 2^{2} - 1 = 3 \\ ∴ f (1) \neq f (2) \end{array}$

It is observed that f does not satisfy a condition of the hypothesis of Rolle's Theorem.

Hence, Rolle's Theorem is not applicable for $f (x) = x^{2} - 1$ for $x \in [1, 2]$ .

less

0 0

New answer posted

6 months ago

Maths Binomial Theorem

1. Show that 9ⁿ⁺¹– 8n – 9 is divisible by 64, whenever n is a positive integer.

0 Follower 216 Views

Payal Gupta

Contributor-Level 10

1. For a number x to be divisible by y, we can write x as a factor of y i.e., x = ky where k is some natural number. Thus in order for 9ⁿ⁺¹ – 8n – 9 to be divisible by 64 we need to show that 9ⁿ⁺¹ – 8n – 9 = 64k where k is some natural number.

We have, by binomial theorem

(1 + a)^m = ^mC₀ + ^mC₁ (a) + ^mC₂ (a)² + ^mC₃ (a)³ + ………… + ^mC_m (a)^m

Putting, a = 8 and m = n + 1

(1 + 8)ⁿ⁺¹ = ⁿ⁺¹C₀ + ⁿ⁺¹C₁.8 + ⁿ⁺¹C₂.8² + ⁿ⁺¹C₃.8³ + ……. + ⁿ⁺¹C_n₊₁. (8)ⁿ⁺¹

=> 9ⁿ⁺¹= 1 + (n + 1)8 + 8²* [ⁿ⁺¹C₂ + ⁿ⁺¹C₃.8 + ………. + ⁿ⁺¹C_n₊₁. (8)ⁿ^+1–2] [since, ⁿ⁺¹C₀ = 1, ⁿ⁺¹C₁= n + 1]

=> 9ⁿ⁺¹ = 1 + 8n + 8 + 64 * [ⁿ⁺¹C₂ + ⁿ⁺¹C₃.8 + ……�

...more

0 0

New answer posted

6 months ago

Maths Differential Equations

61. Kindly Consider the following

$y' = \frac{x + y}{x}$

0 Follower 2 Views

Vishal Baghel

Contributor-Level 10

The given D.E. is

$\begin{array}{l} y^{1} = \frac{x + y}{x} \\ = \frac{d y}{d x} = 1 + \frac{y}{x} = f (\frac{y}{x}) \end{array}$

Hence, the given D.E is homogenous.

Let, $y = v x \to \frac{y}{x} = v, s o t h a t, \frac{d y}{d x} = v + \frac{x d v}{d x}$

So, the D.E. becomes

$\begin{array}{l} v + \frac{x d v}{d x} = 1 + v \\ \Rightarrow \frac{x d v}{d x} = 1 \\ \Rightarrow d v = \frac{d x}{x} \end{array}$

Integrating both sides,

$\begin{array}{l} \int d v = \int \frac{d x}{x} \\ v = l o g | x | + c \end{array}$

Putting $v = \frac{y}{x}$ back we get,

$\frac{y}{x} = l o g | x | + c$

0 0

New answer posted

6 months ago

Maths Continuity and Differentiability

112. Verify Rolle's Theorem for the function $f (x) = x^{2} + 2 x - 8, x \in [- 4, 2]$

0 Follower 2 Views

alok kumar singh

Contributor-Level 10

112. Given, $f (x) = x^{2} + 2 x - 8$ , being polynomial function is continuous in $[- 4, 2]$ and also differentiable in $(- 4, 2)$ .

$\begin{array}{l} f (- 4) = {(- 4)}^{2} + 2 (- 4) - 8 \\ = 16 - 8 - 8 \\ = 0 \\ f (2) = {(2)}^{2} + 2 * 2 - 8 \\ = 4 + 4 - 8 \\ = 0 \end{array}$

Therefore, $f (- 4) = f (2) = 0$

The value of $f (x)$ at -4 and 2 coincides.

Rolle's Theorem states that there is a point $c \in (- 4, 2)$ such that $f^{'} (c) = 0$ $f (x) = x^{2} + 2 x - 8$

Therefore, $f^{'} (x) = 2 x + 2$

Hence,

$\begin{array}{l} f^{'} (c) = 0 \\ 2 c + 2 = 0 \\ c = - 1 \end{array}$

Thus, $c = - 1 \in (- 4, 2)$

Hence, Rolle's Theorem is verified.

0 0

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

65k Colleges
1.2k Exams
679k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

Need guidance on career and education? Ask our experts

Your Question

Maths

Questions

Discussions

Active Users

Followers

All

Discussions

Unanswered Questions

Share Your College Life Experience