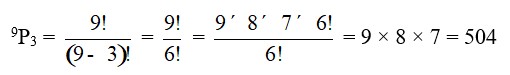Maths
Get insights from 6.5k questions on Maths, answered by students, alumni, and experts. You may also ask and answer any question you like about Maths
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
6 months agoContributor-Level 10
12. The permutation of 9 different digits taken 4 at a time is given by
New answer posted
6 months agoContributor-Level 10
11. i. n = 6, r = 2
=
=
= 30
ii. n = 9, r = 5
=
=
= 9 * 8 * 7 * 6 * 5
= 15,120
New answer posted
6 months agoContributor-Level 10
29. Number of women in the city council n (A) = 6
As there are four men and six women the total number of person in the sample space is 4 + 6 = 10.
So, n (S) = 10
P (A) =
New answer posted
6 months agoContributor-Level 10
28. The sample space of the experiment is
S = { (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5) (6, 6)}
So, n (S) = 12.
(i) Let E be event such that sum of numbers that turn up is 3. Then,
E = { (1, 2)}
So, n (E) = 1
P (E) = .
(ii) Let F be event such that sum of number than turn up is 12. Then,
F = { (6, 6)}
So, n (F) = 1
P (F) = .
New answer posted
6 months agoContributor-Level 10
27. (a) Since there are 52 cards in the sample space,
n (S) = 52.
So, there are 52 sample points.
(b) In a deck of 52 cards there are 4 ace cards of which only one is of spades.
Hence, if A be an event of getting an ace of spades.
n (A) = 1
So, P (A) = .
(c) (i) Let B be an event of drawing an ace. As there are 4 ace cards we have,
n (B) = 4
So, P (B) = .
(ii) Let D be an event of drawing black cards. Since there are 26 black cards we have,
n (D) = 26.
So, P (D) =
New answer posted
6 months agoContributor-Level 10
8. L.H.S = 3! + 4!
= (1 * 2 * 3) + (1 * 2 * 3 * 4)
= 6 + 24
= 30
R.H.S = 7!
= 1 * 2 * 3 * 4 * 5 * 6 * 7
= 5040
As, L.H.S ≠ R.H.S
3! + 4! ≠ 7!
New answer posted
6 months agoContributor-Level 10
1. We know that, n! = n (n – 1) (n – 2)…….
i. 8!
8! = 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8
= 40320
ii. 4! – 3!
= (1 * 2 * 3 * 4) – (1 * 2 * 3)
= 24 – 6
= 18
New answer posted
6 months agoContributor-Level 10
26. The sample space of throwing s dice is
S = {1, 2, 3, 4, 5, 6}, n (S) = 6.
(i) Let A be event such that a prime number will appear. Then,
A = {2, 3, 5}
? n (A) = 3
Here; P (A) =
(ii) Let B be event such that a number greater than or equal to 3 will appear. Then
B = {3, 4, 5, 6}
So, n (B) = 4
Therefore P (B) =
(iii) Let C be event such that a number less than or equal to one will appear. Then,
C = {1}
So, n (C) = 1
? P (C) =
(iv) Let D be event such that a number more than 6 appears. Then,
D =∅
So, n (D) = 0
? P (D) =
(v) Let E be event such that a number less than 6 appears. Then
E = {1, 2, 3, 4, 5}
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 679k Reviews
- 1800k Answers