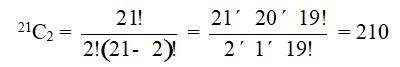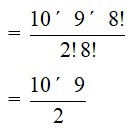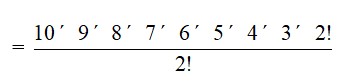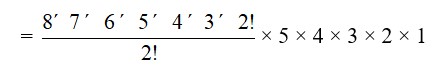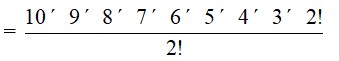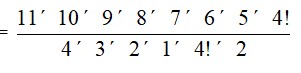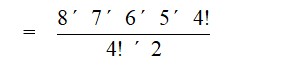Maths

26. In how many ways can a team of 3 boys and 3 girls be selected from 5 boys and 4 girls?

0 Follower 2 Views

Contributor-Level 10

26.The number of ways of selecting a team consisting of 3 boys from 5 boys and 3 girls from 4 girls is

⁵C₃*⁴C₃

= $\frac{5!}{3! (5 - 3)!}$ * $\frac{4!}{3! (4 - 3)!}$

= $\frac{20}{2}$ * $\frac{4}{1}$

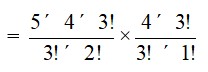
= 40

0 0

New answer posted

6 months ago

25. How many chords can be drawn through 21 points on a circle?

0 Follower 1 View

Contributor-Level 10

25. A chord is drawn by connecting 2 points on a circle.

As we are given with 21 points on the circle, we have the following combination to find the number of chords.

0 0

New answer posted

6 months ago

24. Determine n if (i) ²ⁿC₃ : ⁿC₃ = 12 : 1 (ii) ²ⁿC₃ : ⁿC₃ = 11 : 1

0 Follower 3 Views

Contributor-Level 10

24. i. ²ⁿC₃ : ⁿC₃ = 12 : 1

=> $\frac{2 n!}{3! (2 n - 3)!}$ ÷ $\frac{n!}{3! (n - 3)!}$ = $\frac{12}{1}$

=> $\frac{2 n (2 n - 1) (2 n - 2) (2 n - 3)!}{3! (2 n - 3)!}$ * $\frac{3! (n - 3)!}{n (n - 1) (n - 2) (n - 3)!}$ = 12

=> $\frac{2 n (2 n - 1) (2 n - 2)}{n (n - 1) (n - 2)}$ = 12

=> $\frac{2 (2 n - 1) 2 (n - 1)}{(n - 1) (n - 2)}$ = 12

=> 4(2n - 1) = 12(n – 2)

=> 8n – 4 = 12n – 24

=> 24 – 4 = 12n – 8n

=> 20 = 4n

=>n = $\frac{20}{4}$

=>n = 5

ii. ²ⁿC₃ : ⁿC₃ = 11 : 1

=> $\frac{2 n!}{3! (2 n - 3)!}$ ÷ $\frac{n!}{3! (n - 3)!}$ = $\frac{11}{1}$

=> $\frac{2 n (2 n - 1) (2 n - 2) (2 n - 3)!}{3! (2 n - 3)!}$ * $\frac{3! (n - 3)!}{n (n - 1) (n - 2) (n - 3)!}$ = 11

=> $\frac{2 n (2 n - 1) 2 (n - 1)}{n (n - 1) (n - 2)}$ = 11

=> 4(2n – 1) = 11(n – 2)

=> 8n – 4 = 11n – 22

=> 22 – 4 = 11n – 8n

=> 18 = 3n

=>n = $\frac{18}{3}$

=>n = 6

0 0

New answer posted

6 months ago

54. The number lock of a suitcase has 4 wheels, each labelled with ten digits i.e., from 0 to 9. The lock opens with a sequence of four digits with no repeats. What is the probability of a Person getting the right sequence to open the suitcase?

0 Follower 1 View

Contributor-Level 10

54. Since, the lock can be open by a combination of four digits from the given ten digits I e, from 0 to 9. The number of ways of selecting 4 digits, = 10C₄

This combination of 4 digits can again be arranged within themselves in 41 ways. So, total number of

0 0

New answer posted

6 months ago

53. If 4-digit numbers greater than 5,000 are randomly formed from the digits0, 1, 3, 5, and 7, what is the probability of forming a number divisible by 5 when, (i) The digits are repeated? (ii) The repetition of digits is not allowed?

0 Follower 4 Views

Contributor-Level 10

53. (a) No. of ways of forming a four-digit number greater than 5000 from the given digit 0, 1, 3, 5, 7. and digit repetition is allowed can be done in such a way either 5 or 7 and occupy the thousands' place and any of the digits 0, 1, 3, 5, 7 can occupy the remaining 3 places.

Hence, the required no. of ways = (2* 5 * 5 * 5) - 1

= 250 - 1 = 249

Here 1 is subtracted because 5000 which can be formed by the permutation of the given digits is not allowed

Hence, n (s) = 249.

Similarly, in order to formed a number divisibleby 5 we need to have either 0 or 5 in the one place.

The required number of ways = 2* 5 *5 *2 - 1

= 100 - 1

= 99

...more

Hence, the required no. of ways = (2* 5 * 5 * 5) - 1

= 250 - 1 = 249

Here 1 is subtracted because 5000 which can be formed by the permutation of the given digits is not allowed

Hence, n (s) = 249.

Similarly, in order to formed a number divisibleby 5 we need to have either 0 or 5 in the one place.

The required number of ways = 2* 5 *5 *2 - 1

= 100 - 1

= 99.

Hence, no. of favourable went, n (E) = 99.

Probability that four digit no. greater than 5000 formed by digits 0, 1, 3, 5, 7 (when repetition is) allowed and is divisible by 5 is

P (E) = $\frac{n (E)}{n (s)} = \frac{99}{249} = \frac{33}{83}$

(B) When repetition is not allowed

We can have one of either 7 or 5 on the thousands' place. Then the remaining four other digits can occupy the hundreds, place and then the remaining 3 other digits can occupy tens' places and lastly the remaining 2 other digits can occupy the ones' place.

So, the required number of ways = 2* 4 *3* 2

n (s) = 48

Now, number of 4-digit numbers starting with 5 and divisible by 5 will have 5 on thousands' place and 0 on ones' place then the remaining 3 other digits can fill the hundreds' place and then the remaining 2 other digits can fill the tens' place. So, the required number of ways = 1 *3 *2* 1

= 6

Similarly, 4-digit number starting with 7 divisible by 5 will have 7 on the thousand's place and (one of) 0 or 5 on ones' place. Then the remaining.

3 other digits can fill the hundreds' place and then the remaining 2 other digits can fill the tens' place.

Hence the required no. of ways =1*3* 2 *2=12

So, Total no. of four digit number divisible by 5=6+12=18

Probability that four digit no. greater than 5000 formed

by digits 0,1, 3, 5, 7when repetition is not allowed and is divisible by 5 is

$\frac{18}{48} = \frac{3}{8} .$

less

0 0

New answer posted

6 months ago

Class 11 Permutation and Combinations Exercise 6.4 Solutions

23. ⁿC₈ = ⁿC₂, find ⁿC₂.

0 Follower 11 Views

Contributor-Level 10

23. ⁿC₈ = ⁿC₂

As, ⁿC_a₌ⁿC_b

=>a = b or a = n – b

=>n = a + b

We have,

ⁿC₈ = ⁿC₂

=>n = 8 + 2

=>n = 10

Therefore,

ⁿC₂

= ⁿC₂

= $\frac{10!}{2! (10 ? 2)!}$

= $\frac{10!}{2! 8!}$

= 45

0 0

New answer posted

6 months ago

52. From the employees of a company, 5 persons are selected to represent them inthe managing committee of the company. Particulars of five persons are as follows:

1. No. Name Sex Age in years

2. Harish M 30

3. Rohan M &nbs

...more

0 Follower 3 Views

Contributor-Level 10

52. Total no. of person selected to represent the company n (s) = 5.

Let A: person is male.

A = {Harish, Rohan, Salim}

n (A) = 3

And B: person has one 35 yes of age.

B = {Sheetal, Salim}

n (B) = 2

And A ∩ B = {Salim}

n (A ∩ B) = 1

Probability that person is either male or over 35 years.

= P (A ∪ B) = P (A) + P (B) P (A ∩ B)

$= \frac{n (A)}{n (S)} + \frac{n (B)}{n (S)} - \frac{n (A \cap B)}{n (S)}$

= $= \frac{3}{5} + \frac{2}{5} - \frac{1}{5}$

$= \frac{3 + 2 - 1}{5} = \frac{4}{5}$

0 0

New answer posted

6 months ago

51. A and B are two events such that P(A) = 0.54, P(B) = 0.69 and P(A ∩ B) = 0.35.

Find (i) P(A ∪ B) (ii) P(A´ ∩ B´) (iii) P(A ∩ B´) (iv) P(B ∩ A´)

0 Follower 2 Views

Contributor-Level 10

51. Given, P (A) = 0.54

P (B) = 0.69.

P (A ∩ B) = 0.35.

(i) P (A ∪ B) = P (A) + P (B) - P (A ∩ B)

= 0.54 + 0.69 - 0.35

= 0. 88

(ii) P (A? ∩ B? ) = P (A ∩ B)? = 1 - P (A ∪ B) = 1 - 0.88 = 0.12

(iii) P (A ∩ B? ) = P (A) - P (A ∩ B)

= 0.54 - 0. 35 = 0.19

(iv) P (B ∩ A? ) = P (B) - P (A ∩ B) = 0.69 - 0.35 = 0.34

0 0

New answer posted

6 months ago

22. In how many ways can the letters of the word PERMUTATIONS be arranged if the

(i) Words start with P and end with S,

(ii) Vowels are all together,

(iii) Thereare always 4 letters between P and S?

0 Follower 2 Views

Contributor-Level 10

22. There are 12 letters in which T appears 2 times and rest are all different.

i. When P and S are fixed as first and last letter we can arrange the remaining 10 letter taking all at a time. i.e.

Number of permutation = $\frac{10!}{2!}$

= 18,14,400

ii. We take the 5 vowels (E, U, A, I, O) as one single object. This single object with the remaining 7 object are treated as 8 object which have 2 – T's.

So, number of permutations in which the vowels come together

= permutation of 8 object x permutation within the vowels

= $\frac{8!}{2!}$ * 5!

= 20160 * 120

= 2419200

iii. In order to have 4 letters between P and S, (P, S) should have the possible sets of places (

...more

22. There are 12 letters in which T appears 2 times and rest are all different.

i. When P and S are fixed as first and last letter we can arrange the remaining 10 letter taking all at a time. i.e.

Number of permutation = $\frac{10!}{2!}$

= 18,14,400

ii. We take the 5 vowels (E, U, A, I, O) as one single object. This single object with the remaining 7 object are treated as 8 object which have 2 – T's.

So, number of permutations in which the vowels come together

= permutation of 8 object x permutation within the vowels

= $\frac{8!}{2!}$ * 5!

= 20160 * 120

= 2419200

iii. In order to have 4 letters between P and S, (P, S) should have the possible sets of places (1, 6), (2, 7), (3, 8), (4, 9), (5, 10), (6, 11) and (7, 12) similarly (S, P) should have the same possible sets of places.

So, total number of possible positions fixed for P and S = 14

After fixing P and S we can rearrange the remaining 10 places with the remaining 10 letters of which 2 are T's.

So, required permutation = $\frac{10!}{2!}$

= 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3

= 18,14,400

Therefore, total permutation for which there are always 4 letters between P and S

= 14 * 18,14,400

= 2,54,01,600

less

0 0

New answer posted

6 months ago

21. In how many of the distinct permutations of the letters in MISSISSIPPI do the four I's not come together?

0 Follower 2 Views