Maths

11. Given, A = {1,2,3, …, 14}

R = { (x, y): 3x – y = 0; x, y $\in$ A}

= { (x, y): 3x = y; x, y $\in$ A}.

= { (1,3), (2,6), (3,9), (4,12)}

Domain of R is the set of all the first elements of the ordered pairs in R

So, domain of R= {1,2,3,4}

Codomain of R is the whole set A.

So, codomain of R= {1,2,3, …, 14}

Range of R is the set of all the second elements of the ordered pains in R.

So, range of R= {3,6,9,12}

Exercise 9.3

37.  (i) Given, x + 7y = 0.

7y = -x

y = $\frac{-1}{7}$ x + 0.

Comparing the above equation with y = mx + c we get, slope, m = -$\frac{1}{7}$ and c = 0, y-intercept

(ii) Given, 6x + 3y - 5 = 0

3y = -6x + 5

y = -$\frac{6}{3}$ x + $\frac{5}{3}$ = -2x + $\frac{5}{3}$

Comparing the above equation with y = mx + c we get, slope, m = -2 and $c=\frac{5}{3}$ , y-intercept

(iii) Given, y = 0

y = 0xx + 0

Comparing the above equation with y = mx + c we get, Slope, m = 0 and c = 0, y-intercept.

10. Given, n (A * A)=9

n (A) *n (A) = 9.

n (A)² = 3².

n (A) = 3 .

And (–1,0), (0,1) $\in$ A * A i.e., A * A = { (x, y), x $\in$ A, y $\in$ B}

? A= {–1,0,1}

And A * A= {–1,0,1} * {–1,0,1}

= { (–1, –1), ( –1,0), ( –1,1), (0, –1), (0,0), (0,1), (1, –1), (1,0), (1,1)}

9. Given, n (A)=3

n (B)= 2

So, n (Ax B)=n (A).n (B)=3x 2=6

as (x, 1), (y, 2), (z, 1) ∈Ax B= { (x, y), x∈Aand y∈B}.

A= {x, y, z} and B= {1,2}

As n (A) = 3as n (B) = 2

36. 

Let the given points be A (3, 0), B (–2, –2) and C (8, 2). Then by two point form we can write equation of line passing point A (3, 0) and B (–2, –2) as

$y-y_1=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right)$

$\Rightarrow y-0=\frac{-2-0}{-2-3}\left(x-3\right)$

$\Rightarrow y=\frac{-2}{-5}\left(x-3\right)$

$\Rightarrow 5y=2\left(x-3\right)$

$\Rightarrow 5y=2x-6$

$\Rightarrow 2x-5y-6=0\left(1\right)$

If the three points A, B and C are co-linear, C will also lieonm the line formed by AB or satisfies equation (1).

Hence, putting x = 8 and y = 2 we have

L.H.S. = 2 * 8 – 5 * 2 – 6

= 16 – 10 – 6

= 0 = R.H.S.

The given three points are collinear.

8. A Given, A= {1,2}

B= {3,4}

So, A* B= { (1,3), (1,4), (2,3), (2, 4)}

i.e., n (A *B)=4

A *B will have subset =2⁴=16.They are,

Φ, { (1,3)}, { (1,4)}, { (2, 3)}, { (2,4)}, { (1,3), (1,4)}, { (1,3), (2,3)},

{ (1,3), (2, 4)}, { (1,4), (2, 3)}, { (1,4), (2, 4)}, { (2,3), (2, 4)},

{ (1,3), (1,4), (2, 3)}, { (1,3), (1,4), (2,4)}, { (1,3), (2,3), (2, 4)}, { (1,4), (2,3), (2,4)},

and { (1,3), (1,4), (2,3), (2,4)}

7. Given,

A= {1, 2}, B = {1,2,3,4}, C= {5,6} and D= {5,6,7,8}

(i) L.H. S = A * (B∩ C) = {1,2} [ {1,2,3,4} ∩ {5,6}]

= {1,2}* 

=  .

R.H.S = (A* B)∩ (A *C)= [ {1,2}* {1,2,3,4}]∩ [ {1,2} {5,6}]

= [ { (1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)]∩ [ {1,5), (1,6), (2,5), (2,6)}]

= .

Hence, L.H.S= R.H.S.

(ii) A* C = {1, 2}* {5,6}

= { (1,5), (1,6), (2,5), (2,6)}

B* D = {1,2,3,4} * {5,6,7,8}

= { (1,5), (1,6), (1,7), (1,8), (2,5), (2,6), (2,7), (2,8), (3,5), (3,6), (3,7), (3,8), (4,5), (4,6), (4,7), (4,8)}

As every element of A C is also an element of B* D.

A *C $\subset$ B *D

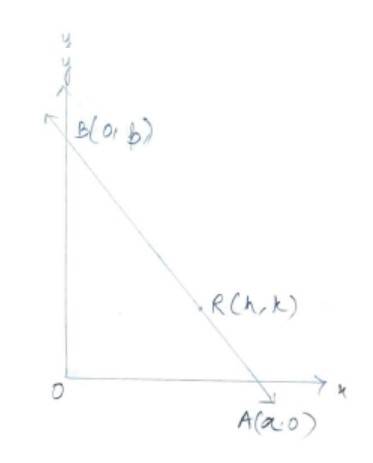
35. Equation of line with intercept form is

$\frac{x}{a}+\frac{y}{b}=1\left(1\right)$

As R (h, x) divides line segment joining point A (a, 0) and B (0, b) in the ratio 1 : 2 we can write,

$\left(h,k\right)=\left(\frac{1*0+2*a}{1+2},\frac{1*b+2*0}{1+2}\right)$

So,  $h=\frac{0+2a}{3}k=\frac{b+0}{3}$

$\Rightarrow \mathrm{3h}=2ab=3k$

$\Rightarrow a=\frac{3h}{2}b=3k$

Hence, putting value of a and b in equation (1) we get,

$\frac{x}{3h/2}+\frac{y}{\mathrm{3k}}=1$

$\Rightarrow \frac{x}{\mathrm{3h}}+\frac{y}{\mathrm{3k}}=1$

6. Given,

A *B = { (a, x), (a, y), (b, x), (b, y)}

We know that,

A *B = { (p, q); p ∈ A and q ∈ B}

So, A = {a, b} and B = {x, y}.