Mechanical Properties of Solids
Get insights from 66 questions on Mechanical Properties of Solids, answered by students, alumni, and experts. You may also ask and answer any question you like about Mechanical Properties of Solids
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
6 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
Consider the diagram according, the bending torque on the trunk of radius r of the tree =
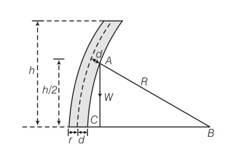
When the tree is about to buckle Wd=
If R>>h, then the centre of gravity is at a height l
From 2+ (h/2)2
If d <2+
So d = h2/8R
If wo is the weight /volume
h= ( )1/3r2/3
critical height = h= ( )1/3r2/3
New answer posted
6 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
l1=AB ,l2=AC ,l3=BC
Cos =
2l3l1cos =
Differentiating 2( )cos -2
= 2
= d
=d
=d
( + )cos + = + -
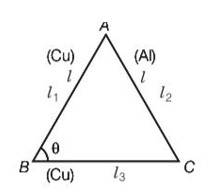
sin (1-cos )-
d
= 2
d = change in the angle ABC
=New answer posted
6 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
Consider an element of width dr at r
Let T(r) and T(r+dr) be the tensions at r+dr respectively
So net centrifugal force = w2rdm
= w2r
T(r)-T(r+dr)= w2rdr
-dT= w2rdr
-
T(r)=
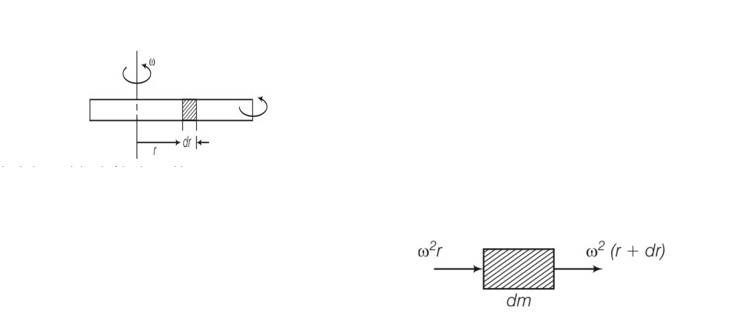
Let the increase in length of the element dr be
So Young's modulus Y= stress/strain=
(l2-r2)
Change in length in right part =
=
Total change in length =
New answer posted
6 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
When a small element of length dx is considered at x from the load x=0
(a) letT(x) and T(x+dx) are tensions on the two cross sections a distance dx apart then
T(x+dx)+T(x)=dmg= dxg
dT= gx+C
at x=0 T(0)=mg
C=mg
T(x)= gx+Mg
Let length dx at x increases by dr then
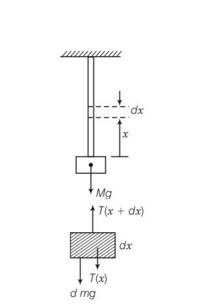
Young's modulus Y= stress/strain
r=
= 0L
r=
so r = 4
(b) tension will be maximum at x=L
T= +Mg=(m+M)g
The force = (yield strength) area=
(m+M)g= 250
Mg
M= 25
New answer posted
6 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
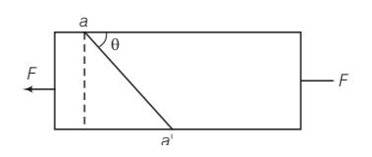
Let the cross sectional area A . consider the equilibrium of the plane aa'. A force F must be acting on this plane making an angle of with the normal ON. Resolving F into components along the plane (FP) and normal to the plane.
By resolving into components
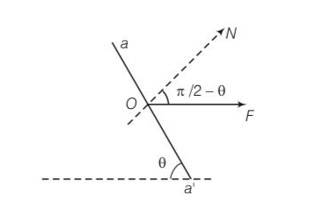
We get Fp= Fcos
And FN= Fsin
Let area of the face aa' be A' then
A/A'=sin so A=A'sin
The tensile stress = normal force/area=Fsin
= sin2
Shearing stress = parallel foce/Area
=
a) For stress to be maximum , sin2 =1
So =
b) Shearing stress to be maximum
sin2
So =
New answer posted
7 months agoContributor-Level 10
Water pressure at the bottom, p = 1.1 Pa
Initial volume of the steel ball, V = 0.32
Bulk modulus of the steel, B = 1.6 N/
The ball falls at the bottom of the Pacific ocean which is 11 km beneath the surface
Let the change in volume of the ball on reaching the bottom of the trench be ΔV
We know, bulk modulus, B = or ΔV =
ΔV = = 2.2
New answer posted
7 months agoContributor-Level 10
Diameter of the metal strip, d = 6.0 mm = 6 m
Radius, r = d/2 = 3 m
Maximum shearing stress = 6.9 Pa =
Maximum force = Maximum stress
= 6.9 = 6.9 = 1950.93 N
Since each rivet carries 1/4th of load,
Maximum tension on each rivet = 4 N = 7803.72 N
New answer posted
7 months agoContributor-Level 10
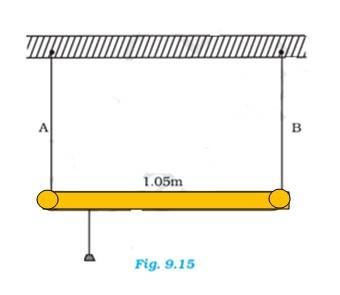
Length of the mild steel wire, l = 1.0 m
Area of cross-section, A = 0.5 = 0.5

A mass of 100 gm is suspended at the midpoint.
m = 100 gm= 0.1 kg
Due to the weight, the wire dips, as shown in the figure.
Original length = XZ, depression = l
The final length of the wire after it dips = XO + OZ
Increase in length of the wire, Δl = (XO + OZ) – XZ ……(i)
From Pythagoras theorem
XO = OZ =
From equation (i)
Δl = 2 - 1.0 = 2 - 1.0 = - 1.0
Neglecting the smaller terms, we can write, Δl =
We know, Strain =
Let T be the tension in the wire, then
mg = 2T
From the figure
=&
New answer posted
7 months agoContributor-Level 10
Cross-sectional area of wire A, = 1 = 1
Cross-sectional area of wire B, = 2 = 2
Young's modulus for steel, = 2 N/
Young's modulus for aluminium, = 7 N/
Stress in the wire = =
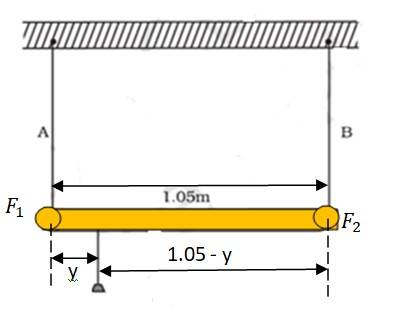
If the two wires have equal stresses, then
= or = = ………(i)
Where is the force exerted on steel wire and is the force exerted on aluminium wire
Taking a moment around the point of suspension, we get
=
= ……(ii)
Using equation (i) and (ii), we can
New answer posted
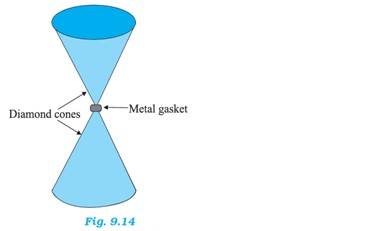
7 months agoContributor-Level 10
Diameter of the cone at the narrow end, d = 0.5 mm = 0.5 m
Radius, r = d/2 = 0.25 m
Area, A = = 1.96
Compressional force, F = 50000 N
Pressure at the tip of the anvil, p = F/A = 50000/1.96 Pa = 2.54 Pa
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers