- Mechanical Properties of Solids Questions and Answers
- qqqqqqqqqqqqqqqqqqqqq
- Jee Mains 2020
Mechanical Properties of Solids Questions and Answers
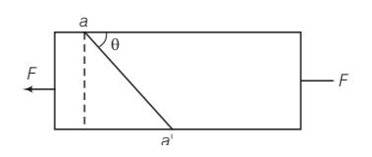
| 1. Consider a long steel bar under a tensile stress due to forces F acting at the edges along the length of the bar (Fig. 9.5). Consider a plane making an angle θ with the length. What are the tensile and shearing stresses on this plane? (a) For what angle is the tensile stress a maximum? (b) For what angle is the shearing stress a maximum?
|
| Explanation- let the cross sectional area A . consider the equilibrium of the plane aa’. A force F must be acting on this plane making an angle of with the normal ON. Resolving F into components along the plane (FP) and normal to the plane. By resolving into components
|
| 2. A steel wire of mass µ per unit length with a circular cross section has a radius of 0.1 cm. The wire is of length 10 m when measured lying horizontal, and hangs from a hook on the wall. A mass of 25 kg is hung from the free end of the wire. Assuming the wire to be uniform and lateral strains << longitudinal strains, find the extension in the length of the wire. The density of steel is 7860 kg m–3 (Young’s modules Y=2×1011 Nm–2). (b) If the yield strength of steel is 2.5×108 Nm–2, what is the maximum weight that can be hung at the lower end of the wire? |
| Explanation- when a small element of length dx is considered at x from the load x=0 (a letT(x) and T(x+dx) are tensions on the two cross sections a distance dx apart then T(x+dx)+T(x)=dmg= dxg dT= gx+C at x=0 T(0)=mg C=mg T(x)= gx+Mg Let length dx at x increases by dr then
|
| 3. A steel rod of length 2l, cross sectional area A and mass M is set rotating in a horizontal plane about an axis passing through the centre. If Y is the Young’s modulus for steel, find the extension in the length of the rod. (Assume the rod is uniform.) |
| Explanation- consider an element of width dr at r Let T(r) and T(r+dr) be the tensions at r+dr respectively So net centrifugal force = w2rdm = w2r T(r)-T(r+dr)= w2rdr -dT= w2rdr - T(r)=
|
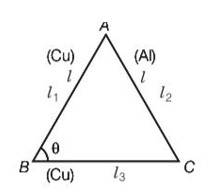
| 4. An equilateral triangle ABC is formed by two Cu rods AB and BC and one Al rod. It is heated in such a way that temperature of each rod increases by ∆T. Find change in the angle ABC. [Coeff. of linear expansion for Cu is α1 ,Coeff. of linear expansion for Al is α2 ] |
| Explanation- l1=AB ,l2=AC ,l3=BC Cos = 2l3l1cos = Differentiating 2( )cos -2 = 2 = d =d =d
( + )cos + = + - |
Commonly asked questions
To what depth must a rubber ball be taken in deep sea so that its volume is decreased by 0.1%. (The bulk modulus of rubber is 9.8×108 N/m2 ; and the density of sea water is 103 kg m-3.)
This is a short answer type question as classified in NCERT Exemplar
Bulk modulus of rubber is 9.8×108 N/m2
density of sea water is 103 kg m-3
percentage decrease in volume
Let the rubber ball be taken up to depth h.
Change in pressure =h g
Bulk modulus K=
So h =
A copper and a steel wire of the same diameter are connected end to end. A deforming force F is applied to this composite wire which causes a total elongation of 1cm. The two wires will have
(a) The same stress.
(b) Different stress.
(c) The same strain.
(d) Different strain.
This is a multiple choice answer as classified in NCERT Exemplar
(a), (d) for steel wire Ysteel= stress/strain=
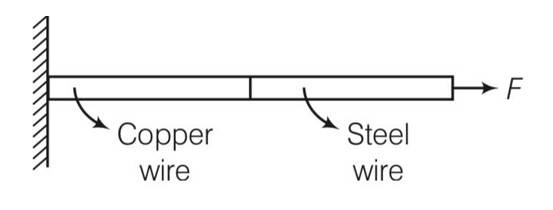
When F and A are same for both the wires . hence stress will be same for both the wire
(Strain)steel= stress/Ysteel and straincopper=stress/Ycopper
Ysteel Ycopper
hence they both have different starin
Consider a long steel bar under a tensile stress due to forces F acting at the edges along the length of the bar (Fig. 9.5). Consider a plane making an angle θ with the length. What are the tensile and shearing stresses on this plane?
(a) For what angle is the tensile stress a maximum?
(b) For what angle is the shearing stress a maximum?
This is a long answer type question as classified in NCERT Exemplar
Let the cross sectional area A . consider the equilibrium of the plane aa’. A force F must be acting on this plane making an angle of with the normal ON. Resolving F into components along the plane (FP) and normal to the plane.
By resolving into components
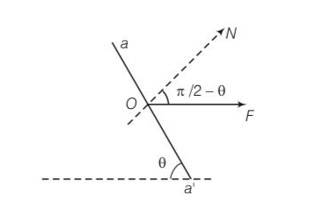
We get Fp= Fcos
And FN= Fsin
Let area of the face aa’ be A’ then
A/A’=sin so A=A’sin
The tensile stress = normal force/area=Fsin
= sin2
Shearing stress = parallel foce/Area
=
a) For stress to be maximum , sin2 =1
So =
b) Shearing stress to be maximum
sin2
So =
A steel wire of mass µ per unit length with a circular cross section has a radius of 0.1 cm. The wire is of length 10 m when measured lying horizontal, and hangs from a hook on the wall. A mass of 25 kg is hung from the free end of the wire. Assuming the wire to be uniform and lateral strains << longitudinal strains, find the extension in the length of the wire. The density of steel is 7860 kg m–3 (Young’s modules Y=2×1011 Nm–2). (b) If the yield strength of steel is 2.5×108 Nm–2, what is the maximum weight that can be hung at the lower end of the wire?
This is a long answer type question as classified in NCERT Exemplar
When a small element of length dx is considered at x from the load x=0
(a) letT(x) and T(x+dx) are tensions on the two cross sections a distance dx apart then
T(x+dx)+T(x)=dmg= dxg
dT= gx+C
at x=0 T(0)=mg
C=mg
T(x)= gx+Mg
Let length dx at x increases by dr then
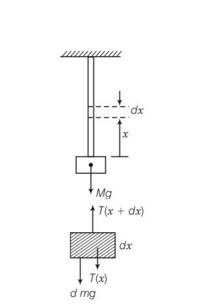
Young’s modulus Y= stress/strain
r=
= 0L
r=
so r = 4
(b) tension will be maximum at x=L
T= +Mg=(m+M)g
The force = (yield strength) area=
(m+M)g= 250
Mg
M= 25
A steel rod of length 2l, cross sectional area A and mass M is set rotating in a horizontal plane about an axis passing through the centre. If Y is the Young’s modulus for steel, find the extension in the length of the rod. (Assume the rod is uniform.)
This is a long answer type question as classified in NCERT Exemplar
Consider an element of width dr at r
Let T(r) and T(r+dr) be the tensions at r+dr respectively
So net centrifugal force = w2rdm
= w2r
T(r)-T(r+dr)= w2rdr
-dT= w2rdr
-
T(r)=
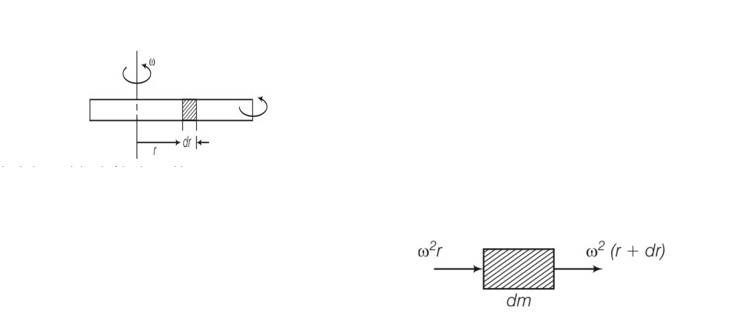
Let the increase in length of the element dr be
So Young’s modulus Y= stress/strain=
(l2-r2)
Change in length in right part =
=
Total change in length =
An equilateral triangle ABC is formed by two Cu rods AB and BC and one Al rod. It is heated in such a way that temperature of each rod increases by ?T. Find change in the angle ABC. [Coeff. of linear expansion for Cu is α1 ,Coeff. of linear expansion for Al is α2 ]
This is a long answer type question as classified in NCERT Exemplar
l1=AB ,l2=AC ,l3=BC
Cos =
2l3l1cos =
Differentiating 2( )cos -2
= 2
= d
=d
=d
( + )cos + = + -
sin (1-cos )-
d
= 2
d = change in the angle ABC
=In nature, the failure of structural members usually result from large torque because of twisting or bending rather than due to tensile or compressive strains. This process of structural breakdown is called buckling and in cases of tall cylindrical structures like trees, the torque is caused by its own weight bending the structure. Thus the vertical through the centre of gravity does not fall within the base. The elastic torque caused because of this bending about the central axis of the tree is given by . Y is the Young’s modulus, r is the radius of the trunk and R is the radius of curvature of the bent surface along the height of the tree containing the centre of gravity (the neutral surface). Estimate the critical height of a tree for a given radius of the trunk.
This is a long answer type question as classified in NCERT Exemplar
Consider the diagram according, the bending torque on the trunk of radius r of the tree =
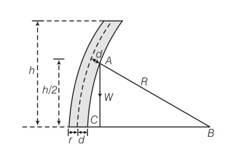
When the tree is about to buckle Wd=
If R>>h, then the centre of gravity is at a height l
From 2+ (h/2)2
If d <2+
So d = h2/8R
If wo is the weight /volume
h= ( )1/3r2/3
critical height = h= ( )1/3r2/3
A stone of mass m is tied to an elastic string of negligible mass and spring constant k. The unstretched length of the string is L and has negligible mass. The other end of the string is fixed to a nail at a point P. Initially the stone is at the same level as the point P. The stone is dropped vertically from point P.
(a) Find the distance y from the top when the mass comes to rest for an instant, for the first time.
(b) What is the maximum velocity attained by the stone in this drop?
(c) What shall be the nature of the motion after the stone has reached its lowest point?
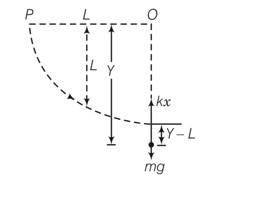
This is a long answer type question as classified in NCERT Exemplar
Till the stone drops through a length L it will be in free fall. After that the elasticity of the spring will force it to a SHM. Let the stone come to rest instantaneously at y.
The loss in PE of the stone is the PE stored in the stretched string .
Mgy=1/2 k(y-L)2
Mgy =
=
Y=
b)in SHM the maximum velocity is attained when the body passes through the equilibrium position i.e when instantaneous acceleration is zero. That is mg-kx=0
so mg=kx
from the conservation of energy
mg=kx
x=mg/k
v2=2gL+mg2/K
v= (2gL+mg2/K)1/2
c)when stone is at lowest position i.e at instantaneous distance Y from p, then equation of motion of the stone is
Make a transformation of variables z=
It is differential equation of second order which represents SHM
Comparing with equation
Anglular frequency of harmonic motion w =
The solution of above equation will be of the type z = Acos (wt+ ) where w =
Y= (L+mg/k)+A’cos(wt+ )
Thus , the stone will perform SHM with angular frequency w= about a point
Yo=L+mg/k
The Young’s modulus for steel is much more than that for rubber. For the same longitudinal strain, which one will have greater tensile stress?
This is a short answer type question as classified in NCERT Exemplar
Young’s modulus Y= stress/longitudinal strain
For same longitudinal strain,
Ysteel>Yrubber
so we can say that stresssteel > stressrubber
Is stress a vector quantity?
This is a short answer type question as classified in NCERT Exemplar
stress=
Therefore stress is scalar quantity not vector quantity.
Identical springs of steel and copper are equally stretched. On which, more work will have to be done?
This is a short answer type question as classified in NCERT Exemplar
Work done =1/2F l
As spring of both are equally compressed
So Young’s modulus Y= as is inversely proportional to young’s modulus
And also we know W is inversely proportional to young’s modulus
So
Wsteel
What is the Young’s modulus for a perfect rigid body ? 9.18 What is the Bulk modulus for a perfect rigid body?
This is a short answer type question as classified in NCERT Exemplar
Young’s modulus Y=
For a perfectly rigid body change in length
Y= so young’s modulus for perfectly rigid body is infinite
A wire of length L and radius r is clamped rigidly at one end. When the other end of the wire is pulled by a force f, its length increases by l. Another wire of the same material of length 2L and radius 2r, is pulled by a force 2f. Find the increase in length of this wire.
This is a short answer type question as classified in NCERT Exemplar
Young’s modulus Y=
For first wire Y=
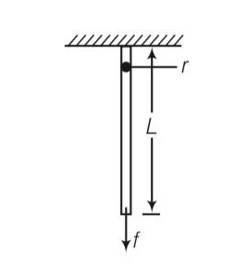
For second wire Y=
From above equations
So l=l’ hence Y will also same.
A steel rod (Y = 2.0 × 1011 Nm-2; and α = 10-50 C-1) of length 1 m and area of cross-section 1 cm2 is heated from 0° C to 200° C, without being allowed to extend or bend. What is the tension produced in the rod?
This is a short answer type question as classified in NCERT Exemplar
Young’s modulus of steel Y= 2
Coefficient of thermal expansion = 10-5
Length =1m
Area = 10-4m2
Increase in temperature t= 2000C
Tension produced in steel rod F = YA =2
= 4
A truck is pulling a car out of a ditch by means of a steel cable that is 9.1 m long and has a radius of 5 mm. When the car just begins to move, the tension in the cable is 800 N. How much has the cable stretched? (Young’s modulus for steel is 2 × 1011 Nm–2.)
This is a short answer type question as classified in NCERT Exemplar
Length of steel cable l=9.1m
Radius r= 5mm=
Tension in the cable F =800N
Young’s modulus of steel Y= 2
So
Two identical solid balls, one of ivory and the other of wet-clay, are dropped from the same height on the floor. Which one will rise to a greater height after striking the floor and why?
This is a short answer type question as classified in NCERT Exemplar
As ivory ball is more elastic than wet clay ball. So ivory ball tries to regain its original shape quickly, hence more energy and momentum transferred to ivory than clay ball. So ivory ball rises high
Modulus of rigidity of ideal liquids is
(a) Infinity
(b) Zero
(c) Unity
(d) Some finite small non-zero constant value
This is a multiple choice answer as classified in NCERT Exemplar
(b) No frictional force exists in case of ideal fluid. Hence tangential forces are zero.
The maximum load a wire can withstand without breaking, when its length is reduced to half of its original length, will
(a) Be double
(b) Be half
(c) Be four times
(d) Remain same
This is a multiple choice answer as classified in NCERT Exemplar
(d) breaking stress = breaking force/area of cross section
Breaking force will not depend upon length.
The temperature of a wire is doubled. The Young’s modulus of elasticity
(a) Will also double
(b) Will become four times
(c) Will remain same
(d) Will decrease
This is a multiple choice answer as classified in NCERT Exemplar
(d) Y young’s modulus is inversely proportional to temperature, so if we increase temperature , young’s modulus decreases.
A spring is stretched by applying a load to its free end. The strain produced in the spring is
(a) Volumetric
(b) Shear
(c) Longitudinal and shear
(d) Longitudinal
This is a multiple choice answer as classified in NCERT Exemplar
(c) Consider the diagram where a spring is stretched by applying a load to its free end. Clearly the length and shape of the spring changes. The change in length corresponds to longitudinal strain and change in shape corresponds to shearing strain.
A rigid bar of mass M is supported symmetrically by three wires each of length l . Those at each end are of copper and the middle one is of iron. The ratio of their diameters, if each is to have the same tension, is equal to
(a) Ycopper /Yiron
(b)
(c)
(d) Yiron/Ycopper .
This is a multiple choice answer as classified in NCERT Exemplar
Y=
D2=
D=
A mild steel wire of length 2L and cross-sectional area A is stretched, well within elastic limit, horizontally between two pillars (Fig. 9.1). A mass m is suspended from the midpoint of the wire. Strain in the wire is
(a)
(b) x/L
(c) x2/2L
(d)
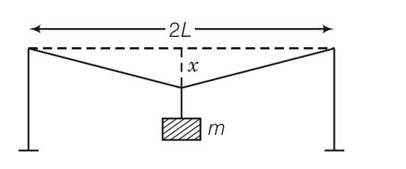
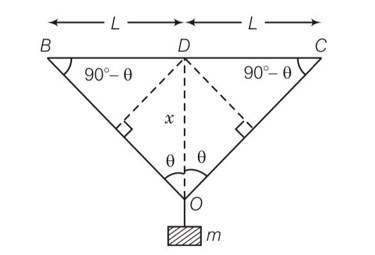
BO+OC- (BD+DC)
= 2BO -2BD
= 2 (BO-BD)
=2 [ (x2+L2)1/2-L]
=2L [ (1+ )1/2-L]
= 2L [ (1+ ]=
Strain =
A rectangular frame is to be suspended symmetrically by two strings of equal length on two supports (Fig. 9.2). It can be done in one of the following three ways The tension in the strings will be
(a) The same in all cases
(b) Least in (a)
(c) Least in (b)
(d) Least in (c)
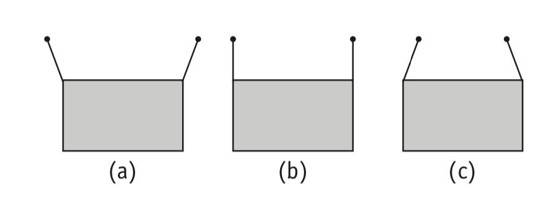
This is a multiple choice answer as classified in NCERT Exemplar
(c) 2Tsin -mg=0
2Tsin =mg
Total horizontal forces = Tcos
T=mg/2sin
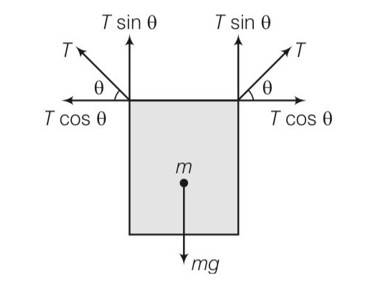
As mg is constant T
Tmax= mg/sin min
Sin min=0, min= 0
Tmin=mg/2sin max
max= 1, =900
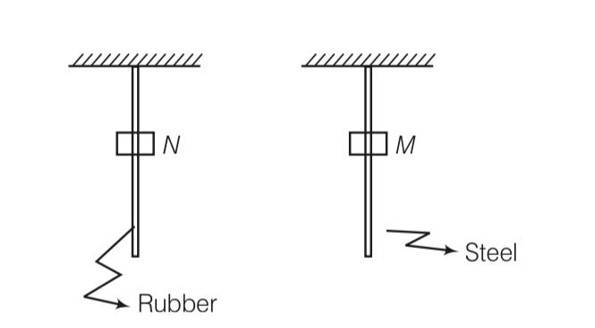
Consider two cylindrical rods of identical dimensions, one of rubber and the other of steel. Both the rods are fixed rigidly at one end to the roof. A mass M is attached to each of the free ends at the centre of the rods.
(a) Both the rods will elongate but there shall be no perceptible change in shape.
(b) The steel rod will elongate and change shape but the rubber rod will only elongate.
(c) The steel rod will elongate without any perceptible change in shape, but the rubber rod will elongate and the shape of the bottom edge will change to an ellipse.
(d) The steel rod will elongate, without any perceptible change in shape, but the rubber rod will elongate with the shape of the bottom edge tapered to a tip at the centre
This is a multiple choice answer as classified in NCERT Exemplar
(d) a mass M is attached at the centre. As the mass is attached to both the rods, both rod will be elongated, but due to different elastic properties of material rubber changes shape also.
The stress-strain graphs for two materials are shown in Fig.9.3 (assume same scale).
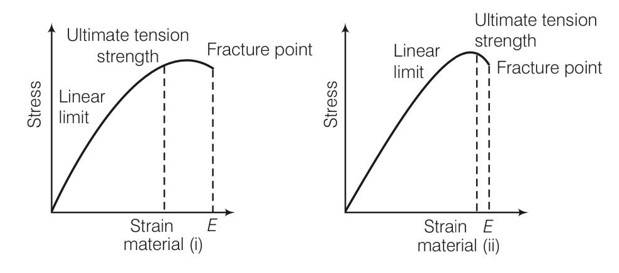
(a) Material (ii) is more elastic than material (i) and hence material (ii) is more brittle.
(b) Material (i) and (ii) have the same elasticity and the same brittleness.
(c) Material (ii) is elastic over a larger region of strain as compared to (i).
(d) Material (ii) is more brittle than material (i).
This is a multiple choice answer as classified in NCERT Exemplar
(c), (d) The ultimate tensile strength for material ii is greater hence material ii is elastic over larger region as compared to material (i) for material (ii) fracture point is nearer, hence it is more brittle.
A wire is suspended from the ceiling and stretched under the action of a weight F suspended from its other end. The force exerted by the ceiling on it is equal and opposite to the weight.
(a) Tensile stress at any cross section A of the wire is F/A
(b) Tensile stress at any cross section is zero
(c) Tensile stress at any cross section A of the wire is 2F/A
(d) Tension at any cross section A of the wire is F
This is a multiple choice answer as classified in NCERT Exemplar
(a), (d) Forces at cross section is F.

Now applying formula . stress = tension/area=F/A
Tension = applied force =F
A rod of length l and negligible mass is suspended at its two ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths (Fig. 9.4). The cross-sectional areas of wires A and B are 1.0 mm2 and 2.0 mm2, respectively. YAl=70 and Ysteel= 200
(a) Mass m should be suspended close to wire A to have equal stresses in both the wires
(b) Mass m should be suspended close to B to have equal stresses in both the wires
(c) Mass m should be suspended at the middle of the wires to have equal stresses in both the wires
(d) Mass m should be suspended close to wire A to have equal strain in both wires
This is a multiple choice answer as classified in NCERT Exemplar
(b), (d) Let mass m is placed at x from the end B respectively.
TA and TB be the tensions in wire A and wire B respectively.
For the rotational equilibrium of the system,
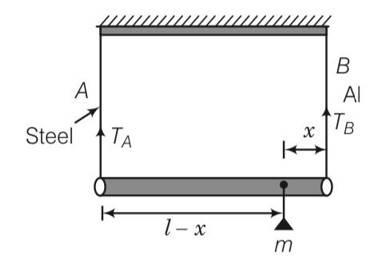
TBx-TA(l-x)=0
=
Stress in wire A = SA=
Stress in wire B = SB= where a are the area of wire
We know that aB=2aA
Now for equal stress
SA=SB
So
So x =l/3 and l-x= 2l/3
Hence mass m should placed to B.
For equal strain
StrainA= StrainB
After solving we get x= x= 10l/17
l-x=l=10l/17=7l/17
For an ideal liquid
(a) The bulk modulus is infinite.
(b) The bulk modulus is zero.
(c) The shear modulus is infinite.
(d) The shear modulus is zero.
This is a multiple choice answer as classified in NCERT Exemplar
(a), (d) An ideal liquid is not compressible
Hence V=0
Bulk modulus B= strss /volumetric strain=
Compressibility K= 1/B=1/
As there is no tangential force exists. So shear strain =0
qqqqqqqqqqqqqqqqqqqqq
qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq
Jee Mains 2020
Jee Mains 2020
Commonly asked questions
12gm of gas occupy a volume of 4 × 10-3 m3 at a temperature of 7°C. After the gas is heated at constant pressure its density becomes 6 × 10-4gm/cm3. What is the temperature to which the gas was heated (in kelvin)?
P = (RT/M? )ρ ⇒ P/ρT = constant
⇒ (12)/ (4 × 10? ³ × 10? ) × 280 = 6 × 10? × T ⇒ T = 1400K
In a young's double slit experiment with monochromatic light, fringes are obtained on a screen placed at some distance from the slits. If the screen is moved 8 cm towards the slits, the change in fringe width is 4 × 10-5 m. If the separation between the slits is 1 mm, find the wavelength of light used (in nm ).
β = (λD/d) ⇒ Δβ = (ΔDλ/d) ⇒ 4 × 10? = (λ/10? ³) × 8 × 10? ² ⇒ λ = 5 × 10? m = 500 nm
A bucket of height 20 cm is placed under a tap such that water flows into the bucket at a constant rate of 100 cm3/s. There is a small hole in the bucket of cross-sectional area of 1 cm2 at height of 3 cm from the bottom. Area of hole is very small as compared to area of the bucket. Find the maximum height (in cm ) above the bottom upto which the water is filled in the bucket. (Take g = 10 m/s2 )
Q = a√2gh
h = Q²/ (a² × 2g) = (10? )²/ (10? × 2 × 10) = 5 cm
Height above the ground = 3 cm + 5 cm = 8 cm
A wooden wheel having radius of 1 m is to be fitted with an iron ring around it. The diameter of the ring is 6 mm smaller than the wooden wheel. If the coefficient of linear expansion of iron is 1.2 × 10-5/ °C, then find the minimum increase in temperature (in °C) to fit the ring on the wheel.
r = r? (1 + αΔT) ⇒ r – r? = r? αΔT
⇒ 3 × 10? ³ = 1 × 1.2 × 10? ΔT ⇒ ΔT = 250°C
A capacitor of capacitance 3µF is charged to a potential difference of 12V. Another identical capacitor, initially uncharged is filled with a dielectric having dielectric constant K and it is connected to the charged capacitor. The final common potential difference across both capacitors is found to be 2V. Find the value of k.
V_common = (C? V? + C? V? )/ (C? + C? )? 2 = (3? F)*12)/ (3? F)+ (3? F)*K)? 2 = 12/ (K+1)? K = 5
Speed of sound in a resonance tube experiment is given by the expression v = 2f0(l2 – l1) where f? is the frequency of the tuning fork and l1, l2 are length of the air column. Consider f0 = 300 Hz with no error in its value. Lengths of the air column l1 and l2 are measured as 25.0 cm and 80.0 cm respectively. Find the absolute error in the speed of sound (in m/s).
Δν = 2f? (Δl? + Δl? ) = 2 × 300 (0.1 + 0.1) × 10? ² = 1.2 m/s
An inductor of inductance 0.1H and a resistor of resistance 8Ω are connected in series to a battery of emf 1.5 V through a switch. Find the initial rate of growth of current when the switch is closed (in A/s).
at t = 0, I = 0; E = L (dI/dt) ⇒ dI/dt = E/L = 1.5/0.1 = 15 A/s
A particle of mass 3 kg moving with speed of 3 m/s is acted upon by an impulse. As a result, the particle starts moving in a direction 90° to the original direction with a speed of 4 m/s. Find the impulse acted upon on the particle in SI units.
I? = P? – P? = 3 × 4? – 3 × 3î = 12? – 9î |I? | = √12² + 9² = 15kgm/s
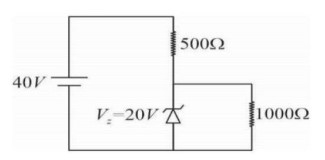
In the given circuit find the current through the Zener diode in mA.
Potential difference across R?
(R? / (R? +R? ) × V is greater than zenor voltage
⇒ i? = V_z/R? = 20/1000 A = 20 mA
Current through R? , i? = (40-V_z)/R? = 20/500 = 40 mA
Current through zener diode = i? - i? = 20 mA
A beam of unpolarized light of intensity I? is incident on a polaroid A. Then it is passed through another polaroid B. If the intensity of the emergent light is 18% of the original unpolarized light then find the angle (nearest integer in degree) between the principal plane of polaroid A and B.
(I? /2)cos²θ = (18/100)I?
⇒ cos²θ = 9/25
⇒ cosθ = 3/5 ⇒ θ = 53°
Physics NCERT Exemplar Solutions Class 11th Chapter Nine Exam