Tags Ncert Solutions Chemistry Class 12th

Ncert Solutions Chemistry Class 12th

Get insights from 2.6k questions on Ncert Solutions Chemistry Class 12th, answered by students, alumni, and experts. You may also ask and answer any question you like about Ncert Solutions Chemistry Class 12th

Follow Ask Question

2.6k

Questions

Discussions

Active Users

Followers

New question posted

5 months ago

Ncert Solutions Chemistry Class 12th Solutions

1. Define the following modes of expressing the concentration of a solution. Which of these modes are independent of temperature and why?

(i) $\frac{w}{w}$ (percentage mass by mass)

(ii) $\frac{V}{V}$ (volume by volume percentage)

(iii) $\frac{w}{V}$ (mass by volume percentage)

(iv) ppm. (parts per million)

(v) x, (mole fraction)

(vi) M (Molarity)

(vii) m (Molality)

0 Follower 2 Views

New answer posted

6 months ago

Ncert Solutions Chemistry Class 12th Chemical Kinetics

4.39 The rate of a reaction quadruples when the temperature changes from 293 K to 313 K. Calculate the energy of activation of the reaction assuming that it does not change with temperature.

0 Follower 9 Views

Payal Gupta

Contributor-Level 10

4.39 Given, k₂ = 4k₁, T₁ = 293K and T₂ = 313K

We know that from the Arrhenius equation, we obtain

On solving, we get,

E_a = 58263.33 J mol^-1 or 58.26 kJ mol^-1

0 0

New answer posted

6 months ago

Ncert Solutions Chemistry Class 12th Chemical Kinetics

4.38 The time required for 10% completion of a first order reaction at 298K is equal to that required for its 25% completion at 308K. If the value of A is 4 * 1010s ^–1, calculate k at 318K and Ea.

0 Follower 7 Views

Payal Gupta

Contributor-Level 10

4.38 We know, time t = (2.303/k) * log ( [R]₀/ [R])

Where, k- rate constant

[R]₀-Initial concentration

[R]-Concentration at time 't'

At 298K, If 10% is completed, then 90% is remaining. t = (2.303/k) * log ( [R]₀/0.9 [R]₀)

t = (2.303/k) * log (1/0.9) t = 0.1054 / k

At temperature 308K, 25% is completed, 75% is remaining t' = (2.303/k') * log ( [R]₀/0.75 [R]₀)

t' = (2.303/k') * log (1/0.75) t' = 2.2877 / k'

But, t = t'

0.1054 / k = 2.2877 / k' / k = 2.7296

From Arrhenius equation, we obtain log k₂/k₁ = (E_a / 2.303 R) * (T₂ - T₁) / T₁T₂

Substituting the values,

E_a = 76640.09 J mol^-1 or 76.64 kJ mol^-1 We know, log k = log A –E_a/RT

Log k =

...more

0 0

New answer posted

6 months ago

Ncert Solutions Chemistry Class 12th Chemical Kinetics

4.37 The decomposition of A into product has value of k as 4.5* 103 s^–1 at 10°C and energy of activation 60 kJ mol^–1. At what temperature would k be 1.5 * 104s^–1?

0 Follower 36 Views

Payal Gupta

Contributor-Level 10

4.37 From Arrhenius equation, we obtain

Also, k₁ = 4.5 * 10³ s ^-¹

T₁ = 273 + 10 = 283 K

k₂ = 1.5 * 10⁴ s ^-¹

E_a = 60 kJ mol ^-¹ = 6.0 * 10⁴ J mol ^-¹

Then,

→ 0.5229 = 3133.627 * (T₂-283)/ (283 * T₂)

→ 0.0472T₂ = T₂-283 T₂ = 297K or T₂ = 24⁰ C

0 0

New answer posted

6 months ago

Ncert Solutions Chemistry Class 12th Chemical Kinetics

4.36 The rate constant for the first order decomposition of H₂O₂ is given by the following equation: log k = 14.34 – 1.25 * 104K/T. Calculate E_a for this reaction and at what temperature will its half-period be 256 minutes?

0 Follower 88 Views

Payal Gupta

Contributor-Level 10

4.36 We know, The Arrhenius equation is given by k = Ae^-Ea/RT Taking natural log on both sides,

Ln k = ln A- (E_a/RT)

Thus, log k = log A - (E_a/2.303RT). eqn 1

The given equation is log k = 14.34 – 1.25 * 10⁴K/T. eqn 2

Comparing 2 equations, E_a/2.303R = 1.25 * 10⁴K

E_a = 1.25 * 10⁴K * 2.303 * 8.314

E_a = 239339.3 J mol^-1 (approximately) E_a = 239.34 kJ mol^-1

Also, when t_1/2 = 256 minutes,

k = 0.693 / t_1/2

= 0.693 / 256

= 2.707 * 10^-3 min^-1 k = 4.51 * 10^-5s^–1

Substitute k = 4.51 * 10^-5s^–1 in eqn 2,

log 4.51 * 10^-5 s^–1 = 14.34 – 1.25 * 10⁴K/T

log (0.654-5) = 14.34– 1.25 * 10⁴K/T = 1.25 * 10⁴/ [ 14.34- log (0.654-5)] T = 668.9K or T =

...more

0 0

New answer posted

6 months ago

Ncert Solutions Chemistry Class 12th Chemical Kinetics

4.35 The decomposition of hydrocarbon follows the equation k = (4.5 * 10¹¹s^–1) e^-28000K/T. Calculate E_a

0 Follower 20 Views

Payal Gupta

Contributor-Level 10

4.35 The given equation is

k = (4.5 x 10¹¹ s^-1) e^-28000^K/T (i)

Comparing, Arrhenius equation

k = Ae ^-E^/RT (ii)

We get, E_a / RT = 28000K / T

⇒E_a = R x 28000K

= 8.314 J K^-1mol^-1 * 28000 K

= 232792 J mol^–1 or 232.792 kJ mol^–1

0 0

New answer posted

6 months ago

Ncert Solutions Chemistry Class 12th Chemical Kinetics

4.34 Sucrose decomposes in acid solution into glucose and fructose according to the first order rate law, with t 1/2 = 3.00 hours. What fraction of sample of sucrose remains after 8 hours?

0 Follower 52 Views

Payal Gupta

Contributor-Level 10

4.34 t_1/2 = 3.00 hours

We know, t_1/2 = 0.693/k

? k = 0.693/3 k = 0.231 hrs^-1

We know, time

Where, k- rate constant

[R]_° -Initial concentration

[R]-Concentration at time 't'

Thus, substituting the values,

log ( [R]₀/ [R]) = 0.8

log ( [R]/ [R]₀) = -0.8

[R]/ [R]₀ = 0.158

Hence, 0.158 fraction of sucrose remains.

0 0

New answer posted

6 months ago

Ncert Solutions Chemistry Class 12th Chemical Kinetics

4.33 Consider a certain reaction A → Products with k = 2.0 * 10 ^–2s ^–1. Calculate the concentration of A remaining after 100 s if the initial concentration of A is 1.0 mol L^–1

0 Follower 33 Views

Payal Gupta

Contributor-Level 10

4.33 Given,

k = 2.0 * 10^–2s^-1

time t = 100s

Concentration [A₀] = 1.0 mol L^-1

We know,

On substituting the values, Log (1/ [A]) = 2.303/2

Log [A] = -2.303/2 [A] = 0.135 mol L^–1

0 0

New answer posted

6 months ago

Ncert Solutions Chemistry Class 12th Chemical Kinetics

4.32 The rate constant for the decomposition of hydrocarbons is 2.418 * 10^–5s ^{– 1} at 546 K. If the energy of activation is 179.9 kJ/mol, what will be the value of pre-exponential factor?

0 Follower 49 Views

Payal Gupta

Contributor-Level 10

4.32 Given,

k = 2.418 * 10^-5 s^-1

T = 546 K

E_a = 179.9 kJ mol^-1 = 179.9 * 10³J mol^-1

The Arrhenius equation is given by k = Ae^-Ea/RT Taking natural log on both sides,

Ln k = ln A- (E_a/RT) Substituting the values,

ln (2.418 * 10^-5 ) = ln A-179.9/ (8.314 * 546)

ln A = 12.5917

A = 3.9 * 10¹² s^-1 (approximately)

0 0

New answer posted

6 months ago

Ncert Solutions Chemistry Class 12th Chemical Kinetics

4.31 The rate constant for the decomposition of N₂O₅ at various temperatures is given below:

Draw a graph between ln k and 1/T and calculate the values of A and Ea . Predict the rate constant at 30° and 50°C.

0 Follower 71 Views

Payal Gupta

Contributor-Level 10

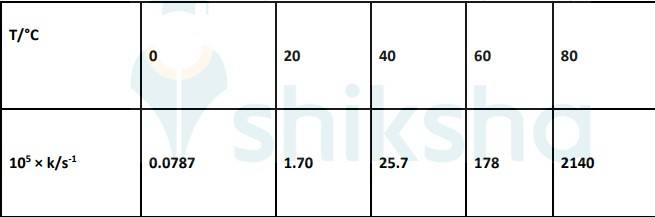
4.31 To convert the temperature in °C to °K we add 273 K.

The graph is given as:

The Arrhenius equation is given by k = Ae^-Ea/RT

Where, k- Rate constant

A- Constant

E_a-Activation Energy

R- Gas constant

T-Temperature

Taking natural log on both sides,

ln k = ln A- (E_a/RT). equation 1

By plotting a graph, ln K Vs 1/T, we get y-intercept as ln A and Slope is –E_a/R.

Slope = (y₂-y₁)/ (x₂-x₁)

By substituting the values, slope = -12.301

? –E_a/R = -12.301

But, R = 8.314 JK^-1mol^-1

? _aE= 8.314 JK^-1mol^-1 * 12.301 K

? _aE= 102.27 kJ mol^-1

Substituting the values in equation 1 for data at T = 273K

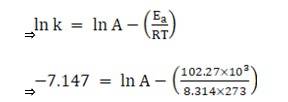
(? At T = 273K, ln k =-7.147)

On solving, we get ln A = 37.

...more

0 0

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

65k Colleges
1.2k Exams
679k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

Need guidance on career and education? Ask our experts

Your Question

Ncert Solutions Chemistry Class 12th

Questions

Discussions

Active Users

Followers

All

Discussions

Unanswered Questions

Share Your College Life Experience