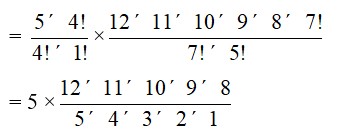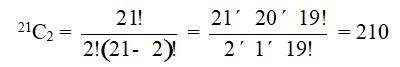Ncert Solutions Maths class 11th

3. $\underset{r\to 1}{lim}\pi r^2=\pi ·{(1)}^2=\pi$

30. We are given 5 black and 6 red balls of which 2 black and 3 red balls can be selected.

Thus the required number of ways

= ^5C₂*⁶C₃

= $\frac{5!}{2!\left(5-2\right)!}$ * $\frac{6!}{3!\left(6-3\right)!}$

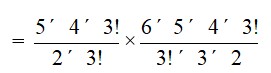
= 10 * 20

= 200

2. $\underset{x\to \pi }{lim}\left(x-\frac{22}{7}\right)=\pi -\frac{22}{7}$

29. We are given 17 players of which 5 players can bowl and 17 – 5 = 12 can bat. But we need to select a team of 11 in which there are exactly 4 bowlers.

Hence, the required number of ways

=⁵C₄ (bowl) x ¹²C _(11-4) (bat)

= $\frac{5!}{4!\left(5-4\right)!}$ * $\frac{12!}{7!\left(12-7\right)!}$

= 5 * 11 * 9 * 8

= 3960

Exercise 13.1

1. 1. $\underset{x\to 3}{lim}$x + 3 = 3 + 3 = 6.

28. In a deck of 52 cards there are 4 ace cards. The required number of ways of selecting one ace card from the four = ⁴C₁ = $\frac{4!}{1!\left(4-1\right)!}$ = $\frac{4!}{3!}$ = $\frac{4*3!}{3!}$ = 4

After selecting one ace we need to select the remaining 4 card from the remaining 48 card to have a combination of 5 cards. The required number of ways

= ⁴⁸C₄

= $\frac{48!}{4!\left(48-4\right)!}$

= 1,94,580

Therefore, the total number of ways for selecting 5 card combination out of a deck of 52 cards if there is exactly one ace in each combination

= ⁴C₁*⁴⁸C₄

= 4 * 1,94,580

= 7,78,320

27. Since we are to select 3 balls from each colour in order to select 9 balls from the collections of 6, 5 and 5 balls of red, white and blue colours respectively, we can have the combination

⁶C₃ (red) *⁵C₃ (white) *⁵C₃ (blue)

= $\frac{6!}{3!\left(6-3\right)!}$ * $\frac{5!}{3!\left(5-3\right)!}$ * $\frac{5!}{3!\left(5-3\right)!}$

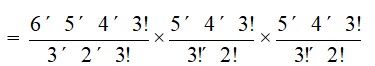
= 20 * 10 * 10

= 2000

26.The number of ways of selecting a team consisting of 3 boys from 5 boys and 3 girls from 4 girls is

⁵C₃*⁴C₃

= $\frac{5!}{3!\left(5-3\right)!}$ * $\frac{4!}{3!\left(4-3\right)!}$

= $\frac{20}{2}$ * $\frac{4}{1}$

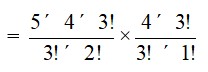
= 40

25. A chord is drawn by connecting 2 points on a circle.

As we are given with 21 points on the circle, we have the following combination to find the number of chords.

24. i. ²ⁿC₃ : ⁿC₃ = 12 : 1

=> $\frac{2n!}{3!\left(2n-3\right)!}$ ÷ $\frac{n!}{3!\left(n-3\right)!}$ = $\frac{12}{1}$

=> $\frac{2n\left(2n-1\right)\left(2n-2\right)\left(2n-3\right)!}{3!\left(2n-3\right)!}$ * $\frac{3!\left(n-3\right)!}{n\left(n-1\right)\left(n-2\right)\left(n-3\right)!}$ = 12

=> $\frac{2n\left(2n-1\right)\left(2n-2\right)}{n\left(n-1\right)\left(n-2\right)}$ = 12

=> $\frac{2\left(2n-1\right)2\left(n-1\right)}{\left(n-1\right)\left(n-2\right)}$ = 12

=> 4(2n - 1) = 12(n – 2)

=> 8n – 4 = 12n – 24

=> 24 – 4 = 12n – 8n

=> 20 = 4n

=>n = $\frac{20}{4}$

=>n = 5

ii. ²ⁿC₃ : ⁿC₃ = 11 : 1

=> $\frac{2n!}{3!\left(2n-3\right)!}$ ÷ $\frac{n!}{3!\left(n-3\right)!}$ = $\frac{11}{1}$

=> $\frac{2n\left(2n-1\right)\left(2n-2\right)\left(2n-3\right)!}{3!\left(2n-3\right)!}$ * $\frac{3!\left(n-3\right)!}{n\left(n-1\right)\left(n-2\right)\left(n-3\right)!}$ = 11

=> $\frac{2n\left(2n-1\right)2\left(n-1\right)}{n\left(n-1\right)\left(n-2\right)}$ = 11

=> 4(2n – 1) = 11(n – 2)

=> 8n – 4 = 11n – 22

=> 22 – 4 = 11n – 8n

=> 18 = 3n

=>n = $\frac{18}{3}$

=>n = 6