Ncert Solutions Maths class 11th
Get insights from 1.6k questions on Ncert Solutions Maths class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about Ncert Solutions Maths class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
9 months agoContributor-Level 10
33. In the word EQUATION, there are vowels (E, U, A, I, O) and 3 consonants (Q, T, N).
Treating vowels as a whole as 1st object and consonants as a whole as 2nd object, we can have an arrangement of 2! = 2.
Similarly, arrangement within the vowels = 5! = 5 * 4 * 3 * 2 * 1 = 120
And arrangement within the consonants = 3! = 3 * 2 * 1 = 6
Therefore, total number of possible arrangement = 2 * 120 * 6 = 1440
New answer posted
9 months agoContributor-Level 10
32. In the word DAUGHTER, there are 3 vowels, namely A, U, E and 5 consonants, namely D, G, H, T, R.
The number of ways of selecting 2 vowels out of 3
= 3C2
=
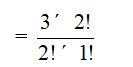
= 3
The number of ways of selecting 3 consonants out of 5
= 5C3
=
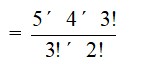
= 5 * 2
= 10
Therefore, the number of combination of 3 consonants and 2 vowels is 3 * 10 = 30.
Each of these 30 combinations has 5 letters which can be arranged among themselves in 5! Ways.
Therefore, the required numbers of different words is
= 30 * 5! = 30 * 5 * 4 * 3 * 2 * 1 = 3600
New answer posted
9 months agoContributor-Level 10
31. A student can choose 5 out of 9 available courses. However 2 specific courses are made compulsory.
So, now a student has 3 choices out of the remaining 7 courses.
Therefore, the required number of ways
=7C3
=
= 35
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 687k Reviews
- 1800k Answers