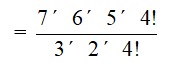Ncert Solutions Maths class 11th

10.$=\underset{z\to 1}{lim}\left[\frac{z^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}-1^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}{z-1}\right]÷\underset{z\to 1}{lim}\left[\frac{z^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}-1^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}}{z-1}\right]$

$=\underset{z\to 1}{lim}\left[\frac{z^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}-1^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}{z-1}\right]÷\underset{z\to 1}{lim}\left[\frac{z^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}-1^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}}{z-1}\right]$

We know that,

$\underset{}{}$$\underset{x\to a}{lim}\frac{x^n-a^n}{x-a}=n{a}^{n-1}$

So,

$=\frac{1}{3}*6=2$

Kindly go through the solution

8.

$=\underset{x\to 3}{lim}\frac{(x+3)(x^2+9)}{2x+1.}$

$=\frac{(3+3)\left(3^2+9\right)}{2*3+1}$

$=\frac{6*18}{6+1}$

$=\frac{108}{7}$

33. In the word EQUATION, there are vowels (E, U, A, I, O) and 3 consonants (Q, T, N).

Treating vowels as a whole as 1st object and consonants as a whole as 2nd object, we can have an arrangement of 2! = 2.

Similarly, arrangement within the vowels = 5! = 5 * 4 * 3 * 2 * 1 = 120

And arrangement within the consonants = 3! = 3 * 2 * 1 = 6

Therefore, total number of possible arrangement = 2 * 120 * 6 = 1440

7.

32. In the word DAUGHTER, there are 3 vowels, namely A, U, E and 5 consonants, namely D, G, H, T, R.

The number of ways of selecting 2 vowels out of 3

= ³C₂

= $\frac{3!}{2!\left(3-2\right)!}$

= 3

The number of ways of selecting 3 consonants out of 5

= ⁵C₃

= $\frac{5!}{3!\left(5-3\right)!}$

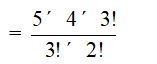
= 5 * 2

= 10

Therefore, the number of combination of 3 consonants and 2 vowels is 3 * 10 = 30.

Each of these 30 combinations has 5 letters which can be arranged among themselves in 5! Ways.

Therefore, the required numbers of different words is

= 30 * 5! = 30 * 5 * 4 * 3 * 2 * 1 = 3600

31. A student can choose 5 out of 9 available courses. However 2 specific courses are made compulsory.

So, now a student has 3 choices out of the remaining 7 courses.

Therefore, the required number of ways

=⁷C₃

= $\frac{7!}{3!\left(7?3\right)!}$

= 35

6. $\underset{x\to 0}{lim}\frac{{(x+1)}^5-1}{x}=\underset{x\to 0}{lim}\frac{x^5+5x^4+10x^3+10x^2+5x+1-1}{}$

Q6. $\underset{x\to 0}{\lim }\frac{{\left(x+1\right)}^5-1}{x}$

6. $\underset{x\to 0}{lim}\frac{{(x+1)}^5-1}{x}=\underset{x\to 0}{lim}\frac{x^5+5x^4+10x^3+10x^2+5x+1-1}{}$ $=\underset{x\to 0}{lim}{x}^4+5x^3+10x^2+10x+5.$ (0)4 + 5(0)3 + 10(0)2 + 10(0) + 5 = 5.

5. $\underset{x\to -1}{lim}\frac{x^{10}+x^5+1}{x-1}=\frac{{(-1)}^{10}+{(-1)}^5+1}{(-1)-1}=\frac{1-1+1}{-2}=-\frac{1}{2}$

4. $\underset{x\to 4}{lim}\frac{4x+3}{x-2}=\frac{4*4+3}{4-2}=\frac{16+3}{2}=\frac{19}{2}$