Ncert Solutions Maths class 11th

33. Assuming the price per litre say P in x-axis and the corresponding demand say D in y-axis, we have two point (14, 980) and (16, 1220) in xy plane. Then the points (P, D) will satisfy the equation.

$\Rightarrow D-980=\frac{1220-980}{16-14}(P-14)$

$\Rightarrow D-980=\frac{240}{2}(P-14)$

$\Rightarrow D-120(P-14)+980$

$\Rightarrow D-12\mathrm{0P}-1680+980$

$\Rightarrow D=12\mathrm{0P}-700$

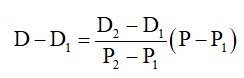
Which is the required relation

Where P = 17, we have

D = 120 * 17 – 700

D = 1340

Hence, the owner can sell 1340 litres of milk weekly at? 17/litre

3. Given, G = {7, 8} and H = {5, 4, 2}

By the definition of the Cartesian product,

G *H = { (x, y): x∈G and y = ∈ H}

= { (7, 5), (7, 4), (7, 2), (8, 5), (8,4), (8,2)}

H* G = { (x, y): x∈ H and y ∈G}

= { (5, 7), (5, 8), (4,7), (4, 8), (2, 7), (2,8)}

2. Given, n (A) = 3

n (B) = 3 or B = {3,4,5}

So, number of elements in A* B = n (A* B) = n (A)* n (B) = 3 *3 = 9.

33. (i) False, as {2,3,4,5} ∩ {3,6} = {3} ≠ $?$ .Hence sets are not disjoint.

(ii) False as {a, e, i, o, u} ∩ {a, b, c, d} = {a} ≠ $?$ Hence sets are not disjoint.

(iii) True as {2,6,10,14} ∩ {3,7,11,15} = $?$ . Hence sets are disjoint.

(iv) True as {2,6,10} ∩ {3,7,11}= $?$ . Hence sets are disjoint.

32. R – Q = {x: x is a real number but not rational number}

= {x: x is an irrational number}

Since real number = rational number + irrational number

31. (i) X – Y = {a, b, c, d} – (f, b, d, g}

= {a, c}

(ii) Y – X = {f, b, d, g} – {a, b, c, d}

= {f, g}

(iii) X ∩ Y = {a, b, c, d} ∩ {f, b, d, g}

= {b, d}.

29. (i) {1,2,3,4} ∩ {x : x is a natural number and 4 ≤ x ≤ 6}

{1, 2, 3, 4} ∩ {4, 5, 6}

{4} ≠∅

Hence, the given pair of set is not disjoint.

(ii) {a, e, i, o, u} ∩ {c, d, e, f}

{e} ≠∅

Hence, the given pair of set is not disjoint.

(iii) {x: x is an even integer} ∩ {x: x is are odd integer}.

=∅

As there is no integer which is both even and odd at the same time.

? Given pair of set are disjoint.

28. A = {1,2,3,4,5, 6, …}

B = {2,4,6, …}

C = {1,3,5, …}

D = {2,3,5, …, }

(i) A ∩ B = {1,2,3,4 …} ∩ {2,4,6, …} = {2,4,6 …} = B.

(ii) A ∩ C = {1,2,3,4, …} ∩ {1,3,5 …} = {1,3,5, …} = C.

(iii) B ∩ C = {2,4,6, …} ∩ {1,3,5, …} = $?$ .

(iv) B ∩ D = {2,4,6 …} ∩ {2,3,5 …} = {2}

(v) C ∩ D = {1,3,5, …} ∩ {2,3,5 …} = {3,5,7 …} = {x : x is odd prime number}