Ncert Solutions Maths class 11th
Get insights from 1.6k questions on Ncert Solutions Maths class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about Ncert Solutions Maths class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
5 months agoContributor-Level 10
35. Let, z = a + ib
=
= [since, (a + b)2 = a2 + b2 + 2ab]
= [since, i2 = –1]
= +
So, |z|2 = a2 + b2
= +
= [since, (a + b)2 = a2 + b2 + 2ab]
=
=
= [as, (a + b)2 = a2 + b2 + 2ab]
Hence proved.
New answer posted
5 months agoContributor-Level 10
34. z1 = 2 – i ,z2 = 1 + i
=
=
=
=
= * [multiply numerator and denominator by (1 + i)]
=
= [since, i2 = –1]
=
=
= |1 + i|
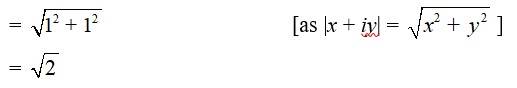
New answer posted
5 months agoContributor-Level 10
33. 21x2 – 28x + 10 = 0
Comparing the given equation with ax2 + bx + c = 0
We have, a = 21, b = –28 andc = 10
Hence, discriminant of the equation is
b2 – 4ac = ( 28)2 – 4 * 21 * 10 = 784 – 840 = –56
Therefore, the solution of the quadratic equation is
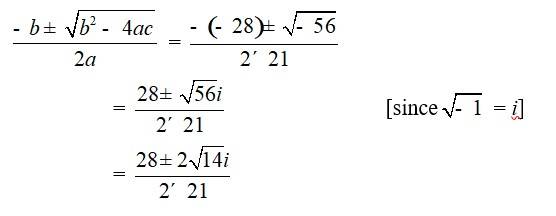
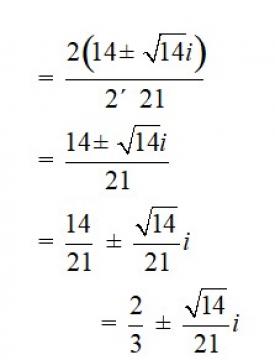
New answer posted
5 months agoContributor-Level 10
32. 27x2 – 10x + 1 = 0
Comparing the given equation with ax2 + bx + c = 0
We have, a = 27, b = –10 andc = 1
Hence, discriminant of the equation is
b2 – 4ac = ( 10)2 – 4 * 27 * 1 = 100 – 108 = –8
Therefore, the solution of the quadratic equation is
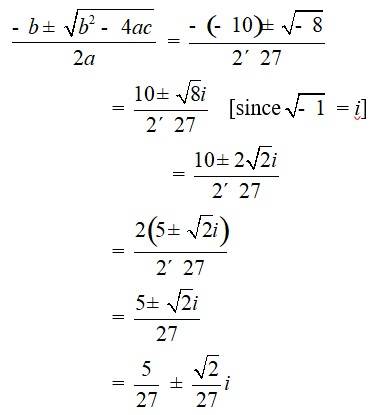
New answer posted
5 months agoContributor-Level 10
31.
![]()
Multiplying the above equation by 2, we get
2x2 - 4x + 3 = 0
and Comparing with ax2 + bx + c = 0
We have, a = 2, b = –4 and c = 3
Hence, discriminant of the equation is
b2 – 4ac = (-4)2 – 4 * 2* 3 = 16 – 24 = –8
Therefore, the solution of the quadratic equation is
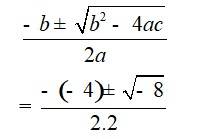
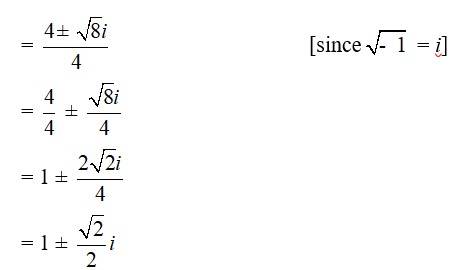
New question posted
5 months agoNew answer posted
5 months agoContributor-Level 10
Multiplying the above equation by 3, we get
9x2 + 12x + 20 = 0
and Comparing with ax2 + bx + c = 0
We have, a =9, b = –12 and c = 20
Hence, discriminant of the equation is
b2 – 4ac = (–12)2 – 4 * 9* 20 = 144 – 720 = –576
Therefore, the solution of the quadratic equation is
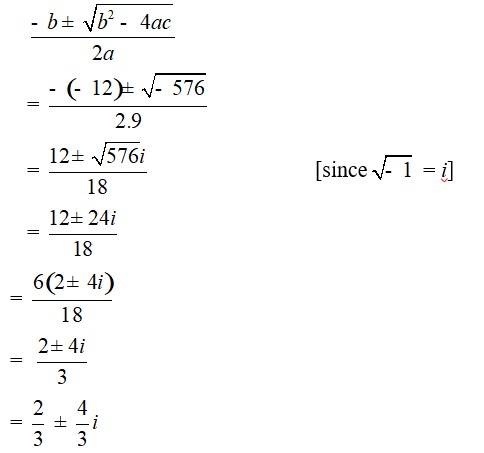
New answer posted
5 months agoContributor-Level 10
29.
=
=
=
=
=
= . [since, i2 = –1]
=
= * [multiplying denominator and numerator by 28 + 10i]
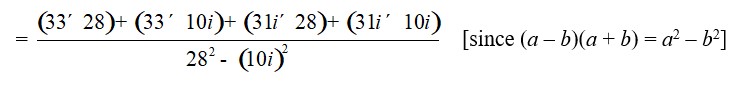
=
= [since, i2 = –1]
=
=
=
= +
New answer posted
5 months agoContributor-Level 10
28. To proof, Re (z1z2) = Re z1 Re z2 – Imz1 Imz2
Let z1 = x1 + iy1 and z2 = x2 + iy2 be two complex number.
Then, z1.z2 = (x1 + iy1) (x2 + iy2)
=x1x2 + ix1y2 + ix2y1 + i2y1y2
= x1x2 + ix1y2 + ix2y1 – y1y2 [since, i2 = -1]
= (x1x2 – y1y2) + i (x1y2 + x2y1)
As, Re (z1z2) = (x1) (x2) – (y1) (y2)
Now, RHS = Re z1 Re z2 – Imz1Imz2 = x1x2 – y1y2
Therefore, Re (z1z2) = Rez1Rez2 – Imz1Imz2
Hence proved.
New answer posted
5 months agoContributor-Level 10
28.
=
= [as i4 *k + 2 = –1 and i4 *k + 1 = i]
=
= [–1 – i]3 [as i2 = –1]
= (-1)3 (1 + i)3
= –1 [13 + i3 + 3 * 1 *i (1 + i)] [since, (a + b)3 = a3 + b3 + 3ab (a + b)]
= –1 [1 – i3 + 3i (1 + i)]
= –1 [1 – i3 + 3i + 3i2]
= –1 [1 – i + 3i – 3] &nb
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 679k Reviews
- 1800k Answers
