Ncert Solutions Maths class 11th

2. Let the given statement be P(n) i.e.,

P(n)=1³+2³+3³+ … +n³= ${\left(\frac{n(n+1)}{2}\right)}^2$

For, n=1, P(n)=1³=1= ${\left(\frac{1(1+1)}{2}\right)}^2={\left(\frac{1.2}{2}\right)}^2=1^2=1$

which is true.

Consider P(k) be true for some positive integer k

1³+2³+3³+ … +k³= ${\left(\frac{k(k+1)}{2}\right)}^2$ ---------- (1)

Now, let us prove that P(k+1) is true.

Here,  1³+2³+3³+ … +k³+(k+1)³

By using eq (1)

= ${\left(\frac{k(k+1)}{2}\right)}^2+{(k+1)}^3$

= $\frac{k^2(k+1){}^2+4·{(k+1)}^3}{4}$

= $\frac{{(k+1)}^2\left[k^2+4(k+1)\right]}{4}$

= $\frac{{(k+1)}^2\left\{k^2+4k+4\right\}}{4}=\frac{{(k+1)}^2(k+2){}^2}{4}$

= ${\left\{\frac{(k+1)(k+1+1)}{2}\right\}}^2$

? P(k+1) is true whenever P(k) is true.

Hence, from the principle of mathematical induction, P(n) is true for all natural numbers n.

1. Let the given statement be P(n) i.e.,

P(n): 1+3+3²+ …+3^n-1= $\frac{\left(3^n-1\right)}{2}$

For n=1, P(1)=1= $\frac{\left(3^1-1\right)}{2}=\frac{3-1}{2}=\frac{2}{2}=1$

which is true.

Assume that P(k) is true for some positive integer k i.e.,

1+3+3²+ … +3^k–1= $\frac{\left(3^k-1\right)}{2}$

--------(1)

Now, let us prove that P(k+1) is true.

Here, 1+3+3²+ … +3^k–1+3^(k+1)–1

$\frac{3^k-1}{2}+3^{k+1-1}$

[By using eq (1)]

= $\frac{3^k-1+2\left(3^{k+\cancel{1}-\cancel{1}}\right)}{2}$

= $\frac{3^k+2.3^k-1}{2}$

= $\frac{3^k(1+2)-1}{2}$

= $\frac{3^k·3-1}{2}=\frac{3^{k+1}-1}{2}$

? P(k+1) is true whenever P(k) is true.

Hence, from the principle of mathematical induction, the P(n) is true for all natural numbers n.

42. We have,

${\left(\frac{1+i}{1-i}\right)}^m$ = 1

=> ${\left(\frac{1+i}{1-i} *\frac{1+}{1+}\right)}^m$ = 1 [multiply denominator and numerator of LHS by (1 + i)]

=> ${\left(\frac{1+i+i+i^2}{1^2- i^2}\right)}^m$ = 1 [since, (a – b) (a + b) = a² – b²]

=> ${\left(\frac{1+2i-1}{1+1}\right)}^m$ = 1 [since, i² = –1]

=> ${\left(\frac{2i}{2}\right)}^m$ = 1

=>i^m = 1

=>i^m = i^4k              [since, i^4k = 1]

So, m = 4k where k = integer

Therefore, least positive integral value of m is,

m = 4 * 1

m = 4

41. Given,

(a + ib) (c + id) (e + if) (g + ih) = A + iB

We know that,

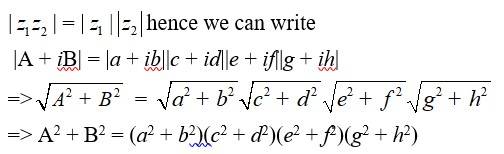
Hence proved.

40.

So, the only solution of the given equation is 0.

Hence, there is no non – zero integral solution of the given equation.

39. (x + iy)³ = u + iv

=>x³ + (iy)³ + 3.x.iy (x + iy) = u + iv   [since, (a + b)³ = a³ + b³ + 3ab (a + b)]

=>x³ – iy³ + 3x²yi + 3xy²i² = u + iv

=>x³ – iy³ + 3x²yi – 3xy² = u + iv                [since, i² = -1]

=> (x³ – 3xy²) + i (3x²y – y³) = u + iv

Equating real and imaginary part we get,

u = x³ – 3xy² and v = 3x²y – y³

Now,  $\frac{u}{x}$ + $\frac{v}{y}$

= $\frac{x^3-3x{y}^2}{x}$ + $\frac{3x^{2}y- y^3}{y}$

= $\frac{x\left(x^2- 3y^2\right)}{x}$ + $\frac{y\left(3x^2- y^2\right)}{y}$

= x² – 3y² + 3x² – y²

= 4x² – 4y²

= 4 (x² – y²)

Hence proved.

38. $\frac{1+i}{1-i}$ – $\frac{1-i}{1+i}$

= $\frac{{\left(1+i\right)}^2- {\left(1-i\right)}^2}{\left(1-i\right)\left(1+i\right)}$

= $\frac{1^2+i^2+2.1.i –\left(1^2+i^2- 2.1.i\right)}{1^2- i^2}$ [Since, (a + b)² = a² + b² + 2ab

(a – b)² = a² + b² – 2ab

a² – b² = (a + b) (a – b)]

= $\frac{1-1+2i-1+1+2i}{1+1}$ [Since, i² = –1]

= $\frac{4i}{2}$

= 2i

37. Let z = (x – iy) (3 + 5i)

= 3x + 5xi – 3yi – 5yi²

= (3x + 5y) + (5x – 3y)i

Given,  $\overline{z}$ = –6 – 24i

=> (3x + 5y) – (5x – 3y)i = –6 – 24i

Equating real and imaginary part,

3x + 5y = –6 - (1)

5x – 3y = 24 - (2)

Multiplying (1) by 3 and (2) by 5 and adding them, we get

9x + 15y + 25x – 15y = –18 + 120

=> 34x = 102

=>x = 102/34 = 3

Putting x = 3 in (1) we get,

3 * 3 + 5y = –6

=> 9 + 5y = –6

=> 5y = –6 – 9

=> 5y = –15

=>y = –15/5 = –3

Hence, the values of x and y are 3 and –3 respectively.

36.  Z₁ = 2 – i, z₂ = –2 + i

Z₁z₂ = (2 – i)(–2 + i)

= –4 + 2i + 2i – i2

= –4 + 4i + 1[since, i² = –1]

= –3 + 4i

$\overline{z_1}$ = 2 + i

i. $\frac{z_1{z}_2}{\overline{z_1}}$ = $\frac{- 3+4i}{2+i}$

= $\frac{-3+4i}{2+i}$ * $\frac{2-i}{2-i}$ [multiply denominator and numerator by (2 – i)]

= $\frac{-6+3i+8i-4i^2}{2^2- i^2}$

= $\frac{-6+11i+4}{4-\left(-1\right)}$ [since, i2 = –1]

= $\frac{-6+4+11i}{4+1 }$

= $\frac{-2+11i}{5}$

= $\frac{-2}{5}$ + $\frac{11}{5}i$

So, Re( $\frac{z_1{z}_2}{\overline{z_1}}$ ) = $\frac{-2}{5}$

ii. $\frac{1}{z_1\overline{z_1}}$ = $\frac{1}{\left(2-i\right)\left(2+i\right)}$

= $\frac{1}{2^2- i^2}$

= $\frac{1}{4+1}$ [since, i2 = –1]

= $\frac{1}{5}$ + 0i

Therefore, Im $\left(\frac{1}{z_1\overline{z_1}}\right)$ = 0