Ncert Solutions Maths class 11th

4. Let a⁵b⁷ occurs in (r + 1)^th term of [removed]a – 2b)¹².

Now, T_r+1 = ¹²C_ra^12-r (–2b)^r

= (–1)^r12C_ra^12–r . 2^r. b^r

Comparing indices of a and b in T_r-1 with a⁵ and b⁷ we get,  r = 7

So, co-efficient of a⁵b⁷ is (–1)⁷¹²C₇ 2⁷

2.

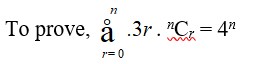
By binomial theorem,

(a + b)ⁿ = ⁿC₀ (a)ⁿ (b)⁰ + ⁿC₁ (a)^n–1 (b)¹ + …………. + ⁿC_r (a)^n–r (b)^r + …………… + ⁿC_n (a)^n–n (b)ⁿ

Where, b⁰ = 1 = a^n–n

So, (a + b)ⁿ = ⁿC_r (a)^n–r (b)^r

Putting a = 1 and b = 3 such that a + b = 4, we can rewrite the above equation as

(1 + 3)ⁿ = ⁿC_r (1)^n–r.3^r

=>4ⁿ = $\underset{r=0}{{\displaystyle ?}}.3r$ .ⁿC_r

Hence proved.

24. Let P (n) be the statement “ 2n+7< (n+3)2

ofn=1

P (1): 2 $*1+7<{(1+3)}^2$

$9<4^2$

9<16 which is true. This P (1) is true.

Suppose P (k) is true.

P (k)= 2k+7< (k+3)^{2   . (1)}              

Lets prove that P (k +1) is also true.

“ 2 (k + 1) + 7 < (k + 4)²=k²+ 8k + 16”

P (k +1) = 2 (k +1) +7 = (2k +7) +2

  < (k +3)²+ 2  (Using 1)

= k²+ 9 + 6k +2 = k²+6k +11

Adding and subtracting (2k + k) in the R. H. S.

$=k^2+6k+11+2k+5-(2k-5)$

$=\left(k^2-8k+16\right)-(2k-5)$

$={(k+4)}^2-(2k-5)$

$<{(k+4)}^2\mathrm{,\; since\; 2}k+5>0$ for all$k\in N$

$\Rightarrow P(k+1)$ is true.

$\therefore$ By the principle of mathematical induction, P (n)is true for all n $\in$ N.

23. Let $P(n):41^n-14^n\mathrm{is\; a\; multiple\; of\; 27.}$

Put n= 1,

$P(1)=41-14=27$ is a multiple of 27.

Which is true.

Assume that P(k) is true for some natural no. k.

P(k)= $41^k-14^k$ be a multiple of 27

i.e, $41^k-14^k=27a,a\in z$

$\Rightarrow 41^k=27a+14^k$ (1)

We want to prove that P(k+1) is also true.

Now,

$P(k+1)=41^{k+1}-14^{k+1}$

$=41^k\cdot 41-14\cdot 14^k$

$=41\left(27a+14^k\right)-14\cdot 14^k$ (Using 1)

$=41*27a+41\cdot 14^k-14\cdot 14^k$

$=-27\left(24+a+14^k\right)=41*27a+14^k(41-14)$

$=41*27a+27\cdot 14^k$

$=27\left(41a+14^k\right)$

$=27b,whereb=\left(41a+14^k\right)\in z$

$\Rightarrow 41^{k+1}-14^{k+1}\mathrm{is\; multiple\; of\; 2}7$

$\Rightarrow P(k+1)$ is true when P(k) is true.

Hence, by P.M.I. P(n) is true for every positive integer n.

22. Let P(n): $3^{2n+2}-8n-9$ is divisible by 8

put n= 1,

P(1): $3^{2+2}-8.1-9$

3⁴ – 8 – 9 = 81– 17 = 64= is divisible by 8

Which is true.

Assume that P(k) is true for some natural numbers k.

i.e, $3^{2k+2}-8k-9$ be divisible by 8

$3^{2k+2}-8k-9=8a$ where,a $\in z$

$3^{2k+2}=8a+8k+9$ (1)

We want to prove thatP(k+ 1) is true.

$P(k+1):3^{2(k+1)+2}-8(k+1)-9$ is divisible by 8, is also true.

Now,

${3^{2k+2+}}^2-=8(k+1)-9$

= $3^{2k+4}-8k+8-9$

$3^{(2k+2)+2}-8k+8-9$

3^{(2k +2)}. 3² $-$ 8k $-$ 17

$=9(8a+8k+9)-8k-17$ (Using 1)

$=72a+72k+81-8k-17$

= 72a + 64k+ 64 = 8(9a + 8k + 8)

= 8b, where b = 9a + 8b + 8 $a\in z$

$\Rightarrow$ 3^{2k + 4}– 8(k+1) – 9 is divisible by 8.

$\therefore$ P(k+1) is true when P(k) is true. Hence, By P.M.I. P(n) is true for all positive integer n.

21. Let 

$\mathrm{Putting\; x}=1,$

$P(1)=x^2-y^2\mathrm{is\; divisible\; by\; x}+y$ or

$\left(x+y\right)(x-y)isdivisiblebyx+y,$ which is true.

Assume that P(k) is true for some natural no. k

$P(k)=x^{2k}-y^{2k}$ is divisible by x + y

i.e. $x^{2k}-y^{2k}=a(x+y)$ where $\in z$

$\Rightarrow x^{2k}=a(x+y)+y^{2k}$ (1)

Now, let us prove P(k +1) is true.

$P(k+1):x^{2(k+1)}-y^{2(k+1)}$

$=x^{2x+2}-y^{2x+2}$

$=x^2\cdot x^{2k}-y^2\cdot y^{2k}$

$=x^2\left[a(x+y)+y^{2k}\right]-y^2\cdot y^{2k}[using(1)$
$]$

$=a{x}^2(x+y)+x^2\cdot y^{2k}-y^2\cdot y^{2k}$

$=a{x}^2(x+y)+y^{2k}\left(x^2-y^2\right)$

$=a{x}^2(x+y)+y^{2k}(x+y)(x-y)$

$=(x+y)\left[a{x}^2+y^{2k}(x-y)\right]$

$=b(x+y)whereb=\left[a{x}^2+y^{2k}(x-y)\right]\in z$

$\Rightarrow x^{2k+2}-y^{2k+2}\mathrm{is\; divisible\; by\; x}+y$

$\therefore$ P(k+ 1) is true where P (k) is true.

Hence, by P.M.I. P(n) is true for all natural number i.e.