Ncert Solutions Maths class 12th
Get insights from 2.5k questions on Ncert Solutions Maths class 12th, answered by students, alumni, and experts. You may also ask and answer any question you like about Ncert Solutions Maths class 12th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
4 months agoContributor-Level 9
AC is collinear with l, m, n.
(l/a) = (m/-a) = (n/4) = λ.
Again (0, -a, -1) lies on lx + my + nz = 0.
l (0) + m (-a) + n (-1) = 0 ⇒ -am - n = 0
-a (-aλ) - (4λ) = 0 ⇒ a²λ - 4λ = 0 ⇒ a² = 4, a = ±2.
for a > 0, a = 2. Direction ratios of BD are 2, -2, 4.
Equation of BD: x/2 = (y - 4)/-2 = (z - 5)/4 = r.
Any point on it (2r, 4 - 2r, 5 + 4r) lies on plane lx + my + nz = 2x - 2y + 4z = 0.
⇒ 4r - 2 (4 - 2r) + 4 (5 + 4r) = 0 ⇒ 24r + 12 = 0 ⇒ r = -1/2.
∴ D (-1, 5, 3), C (0, -2, -1).
∴ CD = √ (0 - (-1)² + (-2 - 5)² + (-1 - 3)²) = √ (1 + 49 + 16) = √66
New answer posted
4 months agoContributor-Level 10
The equation of the line is (x-2)/1 = (y-1)/1 = (z-6)/-2.
Let this be equal to k. So, a point on the line is (k+2, k+1, -2k+6).
This point lies on the plane x + y - 2z = 3.
(k+2) + (k+1) - 2 (-2k+6) = 3
2k + 3 + 4k - 12 = 3
6k - 9 = 3
6k = 12 ⇒ k = 2.
The point of intersection is (2+2, 2+1, -2 (2)+6) = (4, 3, 2).
New answer posted
4 months agoContributor-Level 9
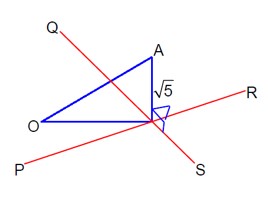
PR (line): r = (3i - j + 2k) + λ (4i - j + 2k) - (I)
QS (line): r = (i + 2j - 4k) + μ (-2i + j - 2k) - (II)
If they intersect at T then:
3 + 4λ = 1 - 2μ
-1 - λ = 2 + μ
2 + 2λ = -4 - 2μ
Solving the first two equations gives λ = 2 & μ = -5. These values satisfy the third equation.
∴ T (11, -3, 6)
Also, OT is coplanar with lines PR and QS.
⇒ TA ⊥ OT
|OT| = √166
|TA| = √5
|OA| = √ (|OT|² + |TA|²) = √171
New answer posted
4 months agoContributor-Level 10
The equation of the circle is x²+y²+ax+2ay+c=0, with a<0.
x-intercept = 2√ (g² - c) = 2√ (a/2)² - c) = 2√2. So, a²/4 - c = 2 => a² = 8 + 4c - (i)
y-intercept = 2√ (f² - c) = 2√ (a² - c) = 2√5. So, a² - c = 5 => a² = 5 + c - (ii)
Equating (i) and (ii): 8 + 4c = 5 + c => 3c = -3 => c = -1.
Substituting c in (ii): a² = 5 - 1 = 4. Since a < 0, a = -2.
The equation of the circle is x² + y² - 2x - 4y - 1 = 0.
Completing the square: (x-1)² + (y-2)² = 1+4+1 = 6.
The center is (1,2) and radius is √6.
The tangent is perpendicular to the line x + 2y = 0 (slope -1/2).
So, the slope of the tangent is 2.
Equation of the tangent: (y-2) = 2 (x-1)
New answer posted
4 months agoContributor-Level 10
The shortest distance D between two skew lines is given by the formula:
D = | (a? - a? ) ⋅ (b? x b? )| / |b? x b? |
Line L? : (x-1)/2 = (y-2)/3 = (z-4)/4
Line L? : (x-2)/3 = (y-4)/4 = (z-5)/5
Here, a? = I + 2j + 4k, b? = 2i + 3j + 4k
a? = 2i + 4j + 5k, b? = 3i + 4j + 5k
a? - a? = I + 2j + k
b? x b? = | I j k |
| 2 3 4 |
| 3 4 5 |
= I (15-16) - j (10-12) + k (8-9) = -i + 2j - k
D = | (i + 2j + k) ⋅ (-i + 2j - k)| / √ (-1)² + 2² + (-1)²)
= |-1 + 4 - 1| / √ (1 + 4 + 1)
= 2 / √6
New answer posted
4 months agoContributor-Level 10
The equation of the plane is given as x + y + z = 42. It is also mentioned that x³ + y³ + z³ = 3xyz.
From the identity, if x³ + y³ + z³ - 3xyz = 0, then x + y + z = 0 or x = y = z.
Given the expression:
3 + (x³ + y³ + z³ - 3xyz) / (xyz)²
Since x³ + y³ + z³ = 3xyz, the expression simplifies to:
3 + 0 = 3
New answer posted
4 months agoContributor-Level 10
P (x) = f (x³) + xg (x³) is divisible by x²+x+1. The roots of x²+x+1=0 are the complex cube roots of unity, ω and ω².
P (ω) = f (ω³) + ωg (ω³) = f (1) + ωg (1) = 0 — (I)
P (ω²) = f (ω²)³) + ω²g (ω²)³) = f (1) + ω²g (1) = 0 — (II)
Subtracting (II) from (I): (ω - ω²)g (1) = 0. Since ω ≠ ω², we must have g (1) = 0.
Substituting g (1)=0 into (I) gives f (1) = 0.
We need to find P (1) = f (1³) + 1*g (1³) = f (1) + g (1).
P (1) = 0 + 0 = 0.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers