Ncert Solutions Maths class 12th

$$77. $A$ is a subset of $B$

$\Rightarrow A\cap B=A$

$\therefore P(A\cap B)=P(B\cap A)=P(A)$

$=P(B/A)=\frac{P(B\cap A)}{P(A)}=1$

$A\cap B\ne 0$

$(A\cap B)=0$

$\Rightarrow P(B/A)=\frac{P(B\cap A)}{P(A)}=0$

76. The repeated tossing of a die are Bernoulli trials. Let X represent the number of times of getting 5 in 7 throws of the die.

Probability of getting 5 in a single throw of the die, p = 1/6

$\therefore q=1-p=1-\frac{1}{6}=\frac{5}{6}$

Clearly, X has the probability distribution with n=7 and $P=\frac{1}{6}$

$\therefore P\left(X=x\right)={\mathrm{nC}}_x$
$q^{n-x}{p}^x={\mathrm{7C}}_x$
$\mathrm{}{\left(\frac{5}{6}\right)}^{7-x}.{\left(\frac{1}{6}\right)}^x$

P (getting 5 exactly twice) $=P\left(X=2\right)$

$={\mathrm{7C}}_2$
$\begin{array}{l}\mathrm{}{\left(\frac{5}{6}\right)}^5.{\left(\frac{1}{6}\right)}^2\\ =21.{\left(\frac{5}{6}\right)}^5.\frac{1}{36}\\ =\left(\frac{7}{12}\right)+{\left(\frac{5}{6}\right)}^5\end{array}$

75. Let X represent the number of winning prizes in 50 lotteries. The trials are Bernoulli trials.

Clearly, X has a binomial distribution with n = 50 and p = 1/100

$\therefore q=1-p=1-\frac{1}{100}=\frac{99}{100}\\ \therefore P\left(X=x\right)={\mathrm{nC}}_x$
$q^{n-x}{p}^x={\mathrm{50C}}_x$
$\begin{array}{l}\mathrm{}{\left(\frac{99}{100}\right)}^{50-x}.{\left(\frac{1}{100}\right)}^x\end{array}$

P (winning at least once) $=P\left(X\ge 1\right)$

$=1-P\left(X<1\right)\\ =1-P\left(X=1\right)\\ =1-{\mathrm{50C}}_0$

$\begin{array}{l}\mathrm{}{\left(\frac{99}{100}\right)}^{50}\\ =1-1.{\left(\frac{99}{100}\right)}^{50}\\ =1-{\left(\frac{99}{100}\right)}^{50}\end{array}$

P (winning exactly once) $=P\left(X=1\right)$

$={\mathrm{50C}}_1$

$\begin{array}{l}\mathrm{}{\left(\frac{99}{100}\right)}^{49}.{\left(\frac{1}{100}\right)}^1\\ =50\left(\frac{1}{100}\right){\left(\frac{99}{100}\right)}^{49}\\ =\frac{1}{2}{\left(\frac{99}{100}\right)}^{49}\end{array}$

P (at least twice) $=P\left(X\ge 2\right)$

$\begin{array}{l}=1-P\left(X<2\right)\\ =1-P\left(X\le 1\right)\\ =1-\left[P\left(X=0\right)+P\left(X=1\right)\right]\\ =\left[1-P\left(X=0\right)\right]-P\left(X=1\right)\\ =1-{\left(\frac{99}{100}\right)}^{50}-\frac{1}{2}.{\left(\frac{99}{100}\right)}^{49}\\ =1-{\left(\frac{99}{100}\right)}^{49}.\left[\frac{99}{100}+\frac{1}{2}\right]\\ =1-{\left(\frac{99}{100}\right)}^{49}.\left(\frac{149}{100}\right)\\ =1-\left(\frac{149}{100}\right){\left(\frac{99}{100}\right)}^{49}\end{array}$

74. The repeated guessing of correct answers from multiple choice questions are Bernoulli trials. Let X represent the number of correct answers by guessing in the set of 5 multiple choice questions.

Probability of getting a correct answer is, p = 1/3

$\therefore q=1-p=1-\frac{1}{3}=\frac{2}{3}$

Clearly, X has a binomial distribution with n=5 and $P=\frac{1}{3}$

$\therefore P=\left(X=x\right)={\mathrm{nC}}_x$
$q^{n-x}{p}^x\\ ={\mathrm{5C}}_x$
$\begin{array}{l}\mathrm{}{\left(\frac{2}{3}\right)}^{5-x}.{\left(\frac{1}{3}\right)}^x\end{array}$

P (guessing more than 4 correct answers) $=P\left(X\ge 4\right)$

$=P\left(X=4\right)+P\left(X=5\right)\\ ={\mathrm{5C}}_4$
$\mathrm{}\left(\frac{2}{3}\right).{\left(\frac{1}{3}\right)}^4+{\mathrm{5C}}_5$
$\begin{array}{l}\mathrm{}{\left(\frac{1}{3}\right)}^5\\ =5.\frac{2}{3}.\frac{1}{81}+1.\frac{1}{243}\\ =\frac{10}{243}+\frac{1}{243}\\ =\frac{11}{243}\end{array}$

73.  X is the random variable whose binomial distribution is B(6,1/2).

Therefore, n = 6 and p = ½

$\therefore q=1-p=1-\frac{1}{2}=\frac{1}{2}\\ Then,P\left(X=x\right)={\mathrm{nC}}_x$
$q^{n-x}{p}^x\\ ={\mathrm{6C}}_x$
$\mathrm{}{\left(\frac{1}{2}\right)}^{6-x}.{\left(\frac{1}{2}\right)}^x\\ ={\mathrm{6C}}_x$
$\begin{array}{l}\mathrm{}{\left(\frac{1}{2}\right)}^6\end{array}$

It can be seen that P (X=x) will be maximum, if ${\mathrm{6C}}_x$
 will be maximum.

$Then,{\mathrm{6C}}_0$
$\mathrm{}={\mathrm{6C}}_6$
$\mathrm{}=\frac{6!}{0!6!}=1\\ {\mathrm{6C}}_1$
$\mathrm{}={\mathrm{6C}}_5$
$\mathrm{}=\frac{6!}{1!5!}=6\\ {\mathrm{6C}}_2$
$\mathrm{}={\mathrm{6C}}_4$
$\mathrm{}=\frac{6!}{2!4!}=15\\ {\mathrm{6C}}_3$
$\begin{array}{l}\mathrm{}=\frac{6!}{3!3!}=20\end{array}$

The value of ${\mathrm{6C}}_3$
 is maximum. Therefore, for x=3, P(X=x) is maximum.

Therefore, P(X=3) is maximum.

72. Let X represent the number of correctly answered questions out of 20 questions.

The repeated tosses of a coin are Bernoulli trails. Since “head” on a coin represents the true answer and “tail” represents the false answer, the correctly answered questions are Bernoulli trials.

$\begin{array}{l}\therefore P=\frac{1}{2}\\ \therefore q=1-p=1-\frac{1}{2}=\frac{1}{2}\end{array}$

X has a binomial distribution with n=20 and $P=\frac{1}{2}$

$\therefore P=\left(X=x\right)={\mathrm{nC}}_x$
$q^{n-x}.p^x,$ where $x=0,1,2,...n$

$={\mathrm{20C}}_x$

$\mathrm{}{\left(\frac{1}{2}\right)}^{20-x}.{\left(\frac{1}{2}\right)}^x\\ ={\mathrm{20C}}_x$
$\begin{array}{l}\mathrm{}{\left(\frac{1}{2}\right)}^{20}\end{array}$

P (at least 12 questions answered correctly) $=P\left(X\ge 12\right)$

$=P\left(X=12\right)+P\left(X=13\right)+...+P\left(X=20\right)\\ ={\mathrm{20C}}_{12}$

$\mathrm{}{\left(\frac{1}{2}\right)}^{20}+{\mathrm{20C}}_{13}$
$\mathrm{}{\left(\frac{1}{2}\right)}^{20}+...+{\mathrm{20C}}_{20}$
$\mathrm{}{\left(\frac{1}{2}\right)}^{20}\\ ={\left(\frac{1}{2}\right)}^{20}.[20C_{12}$
$\mathrm{}+{\mathrm{20C}}_{13}$
$\mathrm{}+...+{\mathrm{20C}}_{20}$
$\begin{array}{l}\mathrm{}]\end{array}$

71. Let X denote the number of balls marked with the digit 0 among the 4 balls drawn.

Since the balls are drawn with replacement, the trials are Bernoulli trials.

X has a binomial distribution with n = 4 and p = 1/10

$\therefore q=1-p=1-\frac{1}{10}=\frac{9}{10}\\ \therefore P\left(X=x\right)={\mathrm{nC}}_x$
$q^{n-x}.p^x,x=1,2,...n\\ ={\mathrm{4C}}_x$
$\begin{array}{l}\mathrm{}{\left(\frac{9}{10}\right)}^{4-x}.{\left(\frac{1}{10}\right)}^x\end{array}$

P (none marked with 0)=P (X=0)

$={\mathrm{4C}}_0$
$\begin{array}{l}\mathrm{}{\left(\frac{9}{10}\right)}^4.{\left(\frac{1}{10}\right)}^0\\ =1.{\left(\frac{9}{10}\right)}^4\\ ={\left(\frac{9}{10}\right)}^4\end{array}$

70. Let X represent the number of bulbs that will fuse after 150 days of use in an experiment of 5 trials. The trials are Bernoulli trials.

It is given that, p = 0.05

$\therefore q=1-p=1-0.05=0.95$

X has a binomial distribution with n=5 and $p=0.05$

$={\mathrm{5C}}_x$
$\mathrm{}{\left(0.95\right)}^{5-x}.{\left(0.05\right)}^x$

$P\left(none\right)=P\left(X=0\right)$

$={\mathrm{5C}}_0$
$\begin{array}{l}\mathrm{}{\left(0.95\right)}^5.{\left(0.05\right)}^0\\ =1*{\left(0.95\right)}^5\\ ={\left(0.95\right)}^5\end{array}$

(ii) P (not more than one) $=P\left(X\le 1\right)$

$=P\left(X=0\right)+P\left(X=1\right)\\ =5C_0$
$\mathrm{}{\left(0.95\right)}^5*{\left(0.05\right)}^0+{\mathrm{5C}}_1$
$\begin{array}{l}\mathrm{}{\left(0.95\right)}^4*{\left(0.05\right)}^1\\ =1*{\left(0.95\right)}^5+5*{\left(0.95\right)}^4*{\left(0.05\right)}^1\\ ={\left(0.95\right)}^5+\left(0.05\right){\left(0.95\right)}^4\\ ={\left(0.95\right)}^4*1.2\end{array}$

(iii) P (more than 1) $=P\left(X>1\right)$

$=1-P\left(X\le 1\right)$

$=1-P$ (not more than 1)

$=1-{\left(0.95\right)}^4*1.2$

(iv) P (at least one) $=P\left(X\ge 1\right)$

$=1-p\left(X<1\right)\\ =1-p\left(X=0\right)\\ =1-{\mathrm{5C}}_0$
$\begin{array}{l}\mathrm{}{\left(0.95\right)}^5*{\left(0.05\right)}^0\\ =1-1*{\left(0.95\right)}^5\\ =1-{\left(0.95\right)}^5\end{array}$

69. Let X represent the number of spade cards among the five cards drawn. Since the drawing of card is with replacement, the trials are Bernoulli trials.

In a well shuffled deck of 52 cards, there are 13 spade cards.

$\begin{array}{l}\Rightarrow p=\frac{13}{52}=\frac{1}{4}\\ \therefore q=1-\frac{1}{4}=\frac{3}{4}\end{array}$

X has a binomial distribution with n=5 and $p=\frac{1}{4}$

$={\mathrm{5C}}_x$
$\mathrm{}{\left(\frac{3}{4}\right)}^{5-x}{\left(\frac{1}{4}\right)}^x$

P (all five cards are spades) $=P\left(X=5\right)$

$={\mathrm{5C}}_5$
$\begin{array}{l}\mathrm{}{\left(\frac{3}{4}\right)}^0.{\left(\frac{1}{4}\right)}^5\\ =1.\frac{1}{1024}\\ =\frac{1}{1024}\end{array}$

(ii) P (only 3 cards are spades) $=P\left(X=3\right)$

$=5C_3$
$\begin{array}{l}\mathrm{}{\left(\frac{3}{4}\right)}^2.{\left(\frac{1}{4}\right)}^3\\ =10.\frac{9}{16}.\frac{1}{64}\\ =\frac{45}{512}\end{array}$

(ii) P (none is a spades) $=P\left(X=0\right)$

$={\mathrm{5C}}_0$
$\begin{array}{l}\mathrm{}{\left(\frac{3}{4}\right)}^5.{\left(\frac{1}{4}\right)}^0\\ =1.\frac{243}{1024}\\ =\frac{243}{1024}\end{array}$

68. Let X denote the number of defective items in a sample of 10 items drawn successively. Since the drawing is done with replacement, the trials are Bernoulli trials.

$\begin{array}{l}\Rightarrow p=\frac{5}{100}=\frac{1}{20}\\ \therefore q=1-\frac{1}{20}=\frac{19}{20}\end{array}$

X has a binomial distribution with n=10 and $p=\frac{1}{20}$

$={\mathrm{10C}}_x$

$\mathrm{}{\left(\frac{19}{20}\right)}^{10-x}.{\left(\frac{1}{20}\right)}^x$

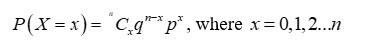
P (not more than 1 defective item) $=P\left(X\le 1\right)$

$=P\left(X=0\right)+P\left(X=1\right)\\ ={\mathrm{10C}}_0$

$\mathrm{}{\left(\frac{19}{20}\right)}^{10}+{\left(\frac{1}{20}\right)}^0+10C_1$
$\begin{array}{l}\mathrm{}{\left(\frac{19}{20}\right)}^9+{\left(\frac{1}{20}\right)}^1\\ ={\left(\frac{19}{20}\right)}^{10}+10{\left(\frac{19}{20}\right)}^9.\left(\frac{1}{20}\right)\\ ={\left(\frac{19}{20}\right)}^9.\left[\frac{19}{20}+\frac{10}{20}\right]\\ ={\left(\frac{19}{20}\right)}^9.\left(\frac{29}{20}\right)\\ =\left(\frac{29}{20}\right).{\left(\frac{19}{20}\right)}^9\end{array}$