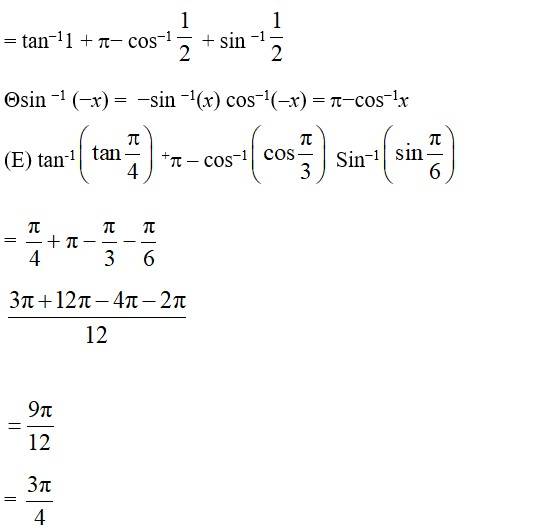Ncert Solutions Maths class 12th

tan⁻¹ (1) + cos⁻¹ $\left(\frac{1}{2}\right)$ +  sin ⁻¹$\left(\frac{-1}{2}\right)$

Let cos ^-1$\left(\frac{-1}{2}\right)$ =y Then cos y = $\frac{-1}{2}$ = − cos
$\frac{\mathrm{}\pi }{3}$$\frac{}{}$ cos $\left(\pi -\frac{x}{3}\right)$

= cos $\frac{3\pi -\pi }{3}$

= cos $\frac{2\pi }{3}$

$$  (E) We know that the range of principal value

branch of cos⁻¹ is [0, $\frac{\pi }{}$] and cos $\frac{2x}{3}$ = $\frac{-1}{2}$

Principal value of cos−1 $\left(\frac{-1}{2}\right)$ is $\frac{2x}{3}$

Let sin⁻¹ $$ $\left(\frac{-1}{2}\right)$ =y. Then, sin y=- $\frac{-1}{2}$

We know that the range of principal value branch of sin⁻¹ is $-\frac{\pi }{2},\;$

and sin⁻¹ $\left(\frac{-1}{2}\right)$ =−sin⁻¹$\frac{-1}{2}$ (sin (-x) = -sin x)

= $\left(-\frac{\pi }{6}\right)$ = sin y (as sin
$\frac{\pi }{6}$
$\frac{}{}$ = $\frac{1}{2}$ )

Principal value of sin⁻¹ $\left(-\frac{1}{2}\right)$ is $\left(-\frac{\pi }{6}\right)$

A binary operation * on {a, b} is a function from {a, b} * {a, b} → {a, b}

i.e., * is a function from { (a, a), (a, b), (b, a), (b, b)} → {a, b}.

Hence, the total number of binary operations on the set {a, b} is 2⁴ i.e., 16.

The correct answer is B.

It is given that,

$f:R\to R$ is defined as $f\left(x\right)=\{\begin{array}{ccc}\hfill 1\hfill & \hfill x>0\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill x=0\hfill & \hfill \hfill \\ \hfill -1\hfill & \hfill x<0\hfill & \hfill \hfill \end{array}$

Also, $g:R\to R$ is defined as $g\left(x\right)=\left[x\right]$ , where [x] is the greatest integer less than or equal to x.

Now, let $x\in \left(0,1\right)$

Then, we have:

$\left[x\right]=1$ if $x=1$ and $\left[x\right]=0$ if $0<x<1$

$\begin{array}{l}\therefore fog\left(x\right)=f\left(g\left(x\right)\right)=f\left(\left[x\right]\right)=\{\begin{array}{cc}\hfill f\left(1\right)\hfill & \hfill if,x=1\hfill \\ \hfill f\left(0\right)\hfill & \hfill if,x\in \left(0,1\right)\hfill \end{array}=\left\{\left(1,"if,x=1"\right),\left(0,:if,x\in \left(0,1\right)"\right):\right\}\\ gof\left(x\right)=g\left(f\left(x\right)\right)\\ =g\left(1\right)\left[x>0\right]\\ =\left[1\right]=1\end{array}$

Thus, when $x\in \left(0,1\right)$ , we have $fog\left(x\right)=0and,gof\left(x\right)=1.$

Hence, fog and gof do not coincide in (0, 1).

Therefore, option (B) is correct.

2, Therefore, option (B) is correct.

It is clear that 1 is reflexive and symmetric but not transitive.

Therefore, option (A) is correct.

It is given that A = {–1, 0, 1, 2}, B = {–4, –2, 0, 2}

Also, it is given that $f,g:A\to B$ are defined by $f\left(x\right)=x^2-x,x\in A$ and $g\left(x\right)=2x-\frac{1}{2}-1,x\in A$ .

It is observed that:

$\begin{array}{l}f\left(-1\right)=\left(1^2\right)-\left(-1\right)=1+1=2\\ g\left(-1\right)=2\left(-1\right)-\frac{1}{2}-1=2\left(\frac{3}{2}\right)-1=3-1=2\\ \Rightarrow f\left(-1\right)=g\left(-1\right)\\ f\left(0\right)={\left(0\right)}^{\wedge }2-0=0\\ g\left(0\right)=2\left(0\right)-\frac{1}{2}-1=2\left(\frac{1}{2}\right)-1=1-1=0\\ \Rightarrow f\left(0\right)=g\left(0\right)\\ f\left(1\right)={\left(1\right)}^{\wedge }2-1=1-1=0\\ g\left(1\right)=2a-\frac{1}{2}-1=2\left(\frac{1}{2}\right)-1=1-1=0\\ \Rightarrow f\left(1\right)=g\left(1\right)\\ f\left(2\right)={\left(2\right)}^{\wedge }2-2=4-2=2\\ g\left(2\right)=2\left(2\right)-\frac{1}{2}-1=2\left(\frac{3}{2}\right)-1=3-1=2\\ \Rightarrow f\left(2\right)=g\left(2\right)\\ \therefore f\left(a\right)=g\left(a\right)\forall a\in A\end{array}$

Hence, the functions f and g are equal.

Let X={0, 1, 2, 3, 4, 5}.

The operation* on X is defined as:

$a*b=\{\begin{array}{cc}\hfill a+b\hfill & \hfill if,a+b<6\hfill \\ \hfill a+b-6\hfill & \hfill if,a+b\ge 6\hfill \end{array}$

An element $e\in X$ is the identity element for the operation*, if $a*e=a=e*a\forall a\in X$

For $a\in X$ we observed that

$\begin{array}{l}a*0=a+0=a\left[a\in X\Rightarrow a+0<6\right]\\ 0*a=0+a=a\left[a\in X\Rightarrow 0+a<6\right]\\ \therefore a*0=0*a\forall a\in X\end{array}$

Thus, 0 is the identity element for the given operation*.

An element $a\in X$ is invertible if there exists $b\in X$ such that $a*0=0*a.$

$ie\{\begin{array}{cc}\hfill a+b=0=b+a\hfill & \hfill if,a+b<6\hfill \\ \hfill a+6-6=0=b+a-6\hfill & \hfill if,a+b\ge 6\hfill \end{array}$

i.e.,

$a=-b,or,b=6-a$

But, X={0, 1, 2, 3, 4, 5} and $a,b\in X$ . Then, $a\ne -b$ .

$\therefore b=6-a$ is the inverse of $a\&mnForE;a\in X.$

Hence, the inverse of an element $a\in X,a\ne 0$ is 6-a i.e., $a^{-1}=6-a.$

It is given that ∗: P (X) * P (X) → P (X) be defined as

 A * B = (A – B) ∪ (B – A), A, B ∈ P (X).

Now, let A? P (X). Then, we get,

A *? = (A –? ) ∪ (? –A) = A∪? = A

? * A = (? - A) ∪ (A -? ) =? ∪A = A

A *? = A =? * A,     A? P (X)

Therefore? is the identity element for the given operation *.

Now, an element A? P (X) will be invertible if there exists B? P (X) such that

A * B =? = B * A. (as? is an identity element.)

Now, we can see that A * A = (A –A) ∪ (A – A) =? ∪? =? A? P (X).

Therefore, all the element A of P (X) are invertible with A-1 = A.