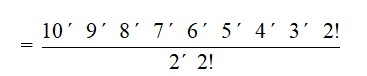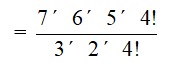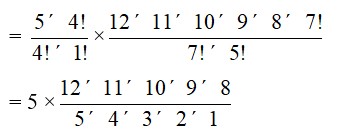Permutations and Combinations

37. Since out of 8 total questions at least 3 questions has to be attempted from each of part I and II containing 5 and 7 questions respectively we can have the choices.

(a) 3 questions from I and 5 questions from II selected in ⁵C₃*⁷C₅ ways.

(b) 4 questions from I and 4 questions from II selected in ⁵C₄*⁷C₄ ways.

(c) 5 questions from I and 3 questions from II selected in ⁵C₅*⁷C₃ ways.

Therefore, the required number of ways.

= (⁵C₃*⁷C₅) + (⁵C₄*⁷C₄) + (⁵C₅*⁷C₃)

= $\frac{5!}{3!\left(5-3\right)!}$ * $\frac{7!}{5!\left(7-5\right)!}$ + $\frac{5!}{4!\left(5-4\right)!}$ * $\frac{7!}{4!\left(7-4\right)!}$ + $\frac{5!}{5!\left(5-5\right)!}$ * $\frac{7!}{3!\left(7-3\right)!}$

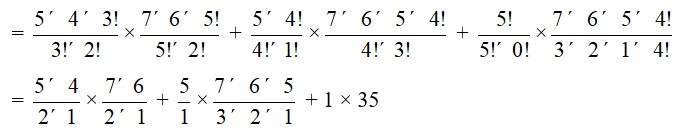
= (10 * 21) + (5 * 35) + 35

= 210 + 175 + 35

= 420

36. In an English word there are 5 vowels and 21 consonants.

The number of ways of selecting 2 vowel out of 5 = ⁵C₂

= $\frac{5!}{2!\left(5?2\right)!}$

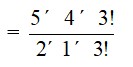
= 5 * 2 = 10

The number of ways of selecting 2 consonants out of 21 = ²¹C₂

= $\frac{21!}{2!\left(21?2\right)!}$

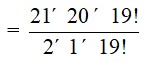
= 21 * 10

= 210

Therefore, the number of combinations of 2 vowels and 2 consonants is 10 * 210 = 2100

Each of these 2100 combinations has 4 letters which can be rearranged among themselves in 4! Ways.

Therefore, the required number of ways

= 4! * 2100

= 4 * 3 * 2 * 1 * 2100

= 50400

35. Since the 6-digit numbers to be formed from the digits 0, 1, 3, 5, 7 and 9 has to be divisible by 10 we have to fix the unit place as 0. Now, the remaining 5 places can be filled only by the digits 1, 3, 5, 7 and 9.

Therefore, the required number of ways

= 5!

= 5 * 4 * 3 * 2 * 1

= 120

34. In the eleven-letter word EXAMINATION there are 2A's, 2I's and 2N's and the rest are all different.

Since in a dictionary the words are listed according to the English alphabet we can only find words starting with A (as B, C, D are not a part of the letters forming the word EXAMINATION) listed before E.

Hence after fixing one A as first word we can rearrange the remaining 10 letters of which 2 are I, 2 are N and rest are all different.

Therefore, the required number of ways = $\frac{10!}{2! 2!}$

= 10 * 9 * 8 * 7 * 6 * 5 * 2 * 3

= 9,07,200

33. In the word EQUATION, there are vowels (E, U, A, I, O) and 3 consonants (Q, T, N).

Treating vowels as a whole as 1st object and consonants as a whole as 2nd object, we can have an arrangement of 2! = 2.

Similarly, arrangement within the vowels = 5! = 5 * 4 * 3 * 2 * 1 = 120

And arrangement within the consonants = 3! = 3 * 2 * 1 = 6

Therefore, total number of possible arrangement = 2 * 120 * 6 = 1440

32. In the word DAUGHTER, there are 3 vowels, namely A, U, E and 5 consonants, namely D, G, H, T, R.

The number of ways of selecting 2 vowels out of 3

= ³C₂

= $\frac{3!}{2!\left(3-2\right)!}$

= 3

The number of ways of selecting 3 consonants out of 5

= ⁵C₃

= $\frac{5!}{3!\left(5-3\right)!}$

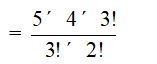
= 5 * 2

= 10

Therefore, the number of combination of 3 consonants and 2 vowels is 3 * 10 = 30.

Each of these 30 combinations has 5 letters which can be arranged among themselves in 5! Ways.

Therefore, the required numbers of different words is

= 30 * 5! = 30 * 5 * 4 * 3 * 2 * 1 = 3600

31. A student can choose 5 out of 9 available courses. However 2 specific courses are made compulsory.

So, now a student has 3 choices out of the remaining 7 courses.

Therefore, the required number of ways

=⁷C₃

= $\frac{7!}{3!\left(7?3\right)!}$

= 35

30. We are given 5 black and 6 red balls of which 2 black and 3 red balls can be selected.

Thus the required number of ways

= ^5C₂*⁶C₃

= $\frac{5!}{2!\left(5-2\right)!}$ * $\frac{6!}{3!\left(6-3\right)!}$

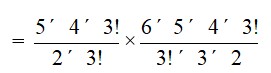
= 10 * 20

= 200

29. We are given 17 players of which 5 players can bowl and 17 – 5 = 12 can bat. But we need to select a team of 11 in which there are exactly 4 bowlers.

Hence, the required number of ways

=⁵C₄ (bowl) x ¹²C _(11-4) (bat)

= $\frac{5!}{4!\left(5-4\right)!}$ * $\frac{12!}{7!\left(12-7\right)!}$

= 5 * 11 * 9 * 8

= 3960

28. In a deck of 52 cards there are 4 ace cards. The required number of ways of selecting one ace card from the four = ⁴C₁ = $\frac{4!}{1!\left(4-1\right)!}$ = $\frac{4!}{3!}$ = $\frac{4*3!}{3!}$ = 4

After selecting one ace we need to select the remaining 4 card from the remaining 48 card to have a combination of 5 cards. The required number of ways

= ⁴⁸C₄

= $\frac{48!}{4!\left(48-4\right)!}$

= 1,94,580

Therefore, the total number of ways for selecting 5 card combination out of a deck of 52 cards if there is exactly one ace in each combination

= ⁴C₁*⁴⁸C₄

= 4 * 1,94,580

= 7,78,320