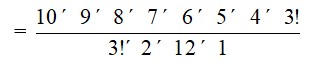Permutations and Combinations

Sum of digits

1 + 2 + 3 + 5 + 6 + 7 = 24

So, either 3 or 6 rejected at a time

Case 1 Last digit is 2

……….2

no. of cases = ²C₁ * 4! = 48

Case 2 Last digit is 6

……….6

= 4! = 24

Total cases = 72

 $A=\left[\begin{array}{ccc}\hfill a_1\hfill & \hfill a_2\hfill & \hfill a_3\hfill \\ \hfill b_1\hfill & \hfill b_2\hfill & \hfill b_3\hfill \\ \hfill c_1\hfill & \hfill c_2\hfill & \hfill c_3\hfill \end{array}\right],a_2,b_2,c_2\in \left\{0,1\right\}$

S = $a_1+a_2+a_3+b_1+b_2+b_3+c_1+c_2+c_3$ is prime

$0\le s\le 9$

Prime value = 2,3, 5, 7

$ForS=2,1+1+0+0+0+0+0+0+0\to \frac{9!}{2!7!}=36$

Total number of matrices

= 36 + 84 + 126 + 36 = 282

We have,  $1-$  (probability of all shots result in failure)  $>\frac{1}{4}$

$\begin{array}{rr}& \Rightarrow 1-{\left(\frac{9}{10}\right)}^{\mathrm{n}}>\frac{1}{4}\\ & \Rightarrow \frac{3}{4}>{\left(\frac{9}{10}\right)}^{\mathrm{n}}\Rightarrow \mathrm{n}\ge 3\end{array}$

$\begin{array}{rr}& D_1=\left|\begin{array}{ccc}-7& 4& -1\\ 8& 1& 5\\ 15& b& 6\end{array}\right|=0\Rightarrow b=-3\\ & D=\left|\begin{array}{ccc}1& 4& -1\\ 3& 1& 5\\ a& b& 6\end{array}\right|=0\Rightarrow 21a-8b-66=0\\ & P:2x-3y+6z=15\end{array}$

so required distance $=\frac{21}{7}=3$

41. In the 13 letter word ASSASSINATION there are 3-A, 4-S, 2-I, 2-N, 1-T and 1-O.

Since all the S are to be occurred together we treat them i.e. (SSSS) as single object. This single object together with 13 – 4 = 9 remaining object will account for 10 objects having 3-A, 2-I, 2-N, 1-T and 1-O and can be rearranged in $\frac{10!}{3!2!2!}$

= 10 * 9 * 8 * 7 * 6 * 5

= 151200

40. In a class of 25 students, 10 students are to be selected for excursion. As 3 students decided that either all of them will join or none of them will join we have the options:

For the 3 students to be selected along with 7 other students from the remaining 25 – 3 = 22 students. This can be done in ³C₃*²²C₇ ways.

For the 3 students to not be selected so that all 10 students will be from the remaining 25 – 3 = 22 students. This can be done in ³C₀*²²C₁₀ ways.

Therefore, the required number of ways

= ³C₃* ²²C₇ + ³C₀*²²C₁₀

= ²²C₇ + ²²C₁₀

39. As out of the total 9 seats 4 women are to be at even places we can have the following arrangement.

Seat places

Also from this arrangement the women and men can rearrange among themselves.

Therefore, the required number of ways = 4! * 5!

= (4 * 3 * 2 * 1) * (5 * 4 * 3 * 2 * 1)

= 24 * 120

= 2880

38. In a deck of 52 card there are four kings.

So, number of ways of selecting exactly one king is ⁴C_1.

Now, after fixing one king card, we need to have the remaining 4 out of 5 cards to be a non-king i.e., only from the other 48 cards. So, number of ways of selecting is ⁴⁸C₄

Therefore, the required number of ways

= ⁴C₁*⁴⁸C₄